题目内容
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )(x∈R)的部分图象如图所示.
)(x∈R)的部分图象如图所示.
(Ⅰ)求函数f(x)的解析式并求函数f(x)的单调递增区间;
(Ⅱ)求函数f(x)的最小值并指出函数f(x)取最小值时相应的x的值.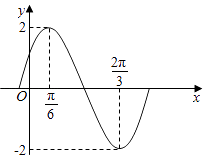
【答案】解:(Ⅰ)由函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )(x∈R)的部分图象可得A=2,最小正周期T=2(
)(x∈R)的部分图象可得A=2,最小正周期T=2( ![]() )=π,得ω=2,可得函数f(x)的解析式为f(x)=2sin(2x+φ),
)=π,得ω=2,可得函数f(x)的解析式为f(x)=2sin(2x+φ),
又f( ![]() )=2,
)=2,
所以sin( ![]() +φ)=1,
+φ)=1,
由于|φ|< ![]() ,可得φ=
,可得φ= ![]() ,
,
所以函数f(x)的解析式为:f(x)=2sin(2x+ ![]() )
)
由于2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,可得kπ﹣
,可得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() (k∈Z),
(k∈Z),
所以函数f(x)的单调递增区间为:[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z),
](k∈Z),
(Ⅱ)函数f(x)的最小值为﹣2,
函数f(x)取最小值﹣2时,有2x+ ![]() =2kπ﹣
=2kπ﹣ ![]() (k∈Z),可得:x=kπ﹣
(k∈Z),可得:x=kπ﹣ ![]() (k∈Z),
(k∈Z),
所以函数f(x)取最小值﹣2时相应的x的值是:x=kπ﹣ ![]() (k∈Z)
(k∈Z)
【解析】(Ⅰ)由图形可确定A,周期T,从而可得ω的值,再由f( ![]() )=2,得2×
)=2,得2× ![]() +φ=
+φ= ![]() +2kπ(k∈Z),进一步结合条件可得φ的值,即可解得f(x)的解析式,由2kπ﹣
+2kπ(k∈Z),进一步结合条件可得φ的值,即可解得f(x)的解析式,由2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,可得函数f(x)的单调递增区间;(Ⅱ)由正弦函数的图象和性质,由2x+
,可得函数f(x)的单调递增区间;(Ⅱ)由正弦函数的图象和性质,由2x+ ![]() =2kπ﹣
=2kπ﹣ ![]() (k∈Z),即可解得函数f(x)的最小值并指出函数f(x)取最小值时相应的x的值.
(k∈Z),即可解得函数f(x)的最小值并指出函数f(x)取最小值时相应的x的值.
【考点精析】关于本题考查的三角函数的最值,需要了解函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能得出正确答案.
才能得出正确答案.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目