题目内容
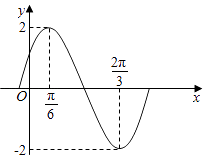
【题目】已知函数![]() ,
,![]() ,其中
,其中![]() 是自然对数的底数.
是自然对数的底数.
(Ⅰ)判断函数![]() 在
在![]() 内零点的个数,并说明理由;
内零点的个数,并说明理由;
(Ⅱ)![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,试求实数
成立,试求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,求证:
,求证:![]() .
.
【答案】(1)1(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(Ⅰ)首先求函数的导数![]() ,判断导数的正负,得到函数的单调性,再根据零点存在性定理得到零点的个数;(Ⅱ)不等式
,判断导数的正负,得到函数的单调性,再根据零点存在性定理得到零点的个数;(Ⅱ)不等式![]() 等价于
等价于![]() ,根据导数分别求两个函数的最小值和最大值,建立不等式求
,根据导数分别求两个函数的最小值和最大值,建立不等式求![]() 的取值范围;(Ⅲ)利用分析法逐步找到使命题成立的充分条件,即
的取值范围;(Ⅲ)利用分析法逐步找到使命题成立的充分条件,即![]() ,证明
,证明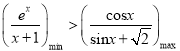 ,求
,求![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)函数![]() 在
在![]() 上的零点的个数为1,,
上的零点的个数为1,,
理由如下:因为![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() .
.
所以函数![]() 在
在![]() 上是单调递增函数.
上是单调递增函数.
因为![]() ,
,![]() ,
,
根据函数零点存在性定理得
函数![]() 在
在![]() 上的零点的个数为1.
上的零点的个数为1.
(Ⅱ)因为不等式![]() 等价于
等价于![]() ,
,
所以![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,等价于
成立,等价于![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在区间
在区间![]() 上单调递增,所以
上单调递增,所以![]() 时,
时,![]() 取得最小值-1,
取得最小值-1,
又![]() ,由于
,由于![]() ,
,![]() ,
,![]() ,
,
所以![]() ,故
,故![]() 在区间
在区间![]() 上单调递增.
上单调递增.
因此,![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
所以![]() ,所以
,所以![]() ,
,
所以实数![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)当![]() 时,要证
时,要证![]() ,只要证
,只要证![]() ,
,
只要证![]()
![]() ,
,
只要证![]() ,
,
由于![]() ,
,![]() 只要证
只要证![]() .
.
下面证明![]() 时,不等式
时,不等式![]() 成立.
成立.
令![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,![]() 是单调递减;
是单调递减;
当![]() 时,
时,![]() ,
,![]() 是单调递增.
是单调递增.
所以当且仅当![]() 时,
时,![]() 取得极小值也就是最小值为1.
取得极小值也就是最小值为1.
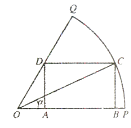
令![]() ,其可看作点
,其可看作点![]() 与点
与点![]() 连线的斜率,
连线的斜率,
所以直线![]() 的方程为:
的方程为:![]() ,
,
由于点![]() 在圆
在圆![]() 上,所以直线
上,所以直线![]() 与圆
与圆![]() 相交或相切,
相交或相切,
当直线![]() 与圆
与圆![]() 相切且切点在第二象限时,
相切且切点在第二象限时,
当直线![]() 取得斜率
取得斜率![]() 的最大值为1.
的最大值为1.
故![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
综上所述,当![]() 时,
时,![]() 成立.
成立.

 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案【题目】中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷影长的记录中,冬至和夏至的晷影长是实测得到的,其他节气的晷影长则是按照等差数列的规律计算得出的.下表为《周髀算经》对二十四节气晷影长的记录,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸=10分).
分(1寸=10分).
节气 | 冬至 | 小寒(大雪) | 大寒(小雪) | 立春(立冬) | 雨水(霜降) | 惊蛰(寒露) | 春分(秋分) |
晷影长(寸) | 135 |
|
|
|
|
| 75.5 |
节气 | 清明(白露) | 谷雨(处暑) | 立夏(立秋) | 小满(大暑) | 芒种(小暑) | 夏至 | |
晷影长(寸) |
|
|
|
|
| 16.0 |
已知《易知》中记录的冬至晷影长为130.0寸,夏至晷影长为14.8寸,那么《易经》中所记录的惊蛰的晷影长应为__________寸.