题目内容
如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=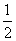 AB=1,M是PB的中点.
AB=1,M是PB的中点.
(1)求证:AM=CM;
(2)若N是PC的中点,求证:DN∥平面AMC.
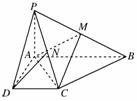
证明: (1)在直角梯形ABCD中,AD=DC=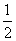 AB=1,∴AC=
AB=1,∴AC=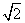 ,BC=
,BC=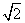 ,∴BC⊥AC,
,∴BC⊥AC,
又PA⊥平面ABCD,BC⊂平面ABCD,
∴BC⊥PA,∴BC⊥平面PAC,∴BC⊥PC.
在Rt△PAB中,M为PB的中点,则AM=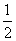 PB,
PB,
在Rt△PBC中,M为PB的中点,则CM=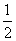 PB,∴AM=CM.
PB,∴AM=CM.
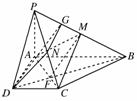
(2)连接DB交AC于点F,
∵DC綊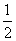 AB,∴DF=
AB,∴DF=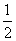 FB.
FB.
取PM的中点G,连接DG,FM,则DG∥FM,
又DG⊄平面AMC,FM⊂平面AMC,
∴DG∥平面AMC.
连接GN,则GN∥MC,
∴GN∥平面AMC,
又GN∩DG=G,
∴平面DNG∥平面AMC.
又DN⊂平面DNG,∴DN∥平面AMC.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =________.
=________.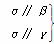 ⇒β∥γ ②
⇒β∥γ ②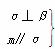 ⇒m⊥β ③
⇒m⊥β ③ ⇒α⊥β ④
⇒α⊥β ④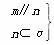 ⇒m∥α
⇒m∥α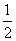 B.
B.
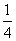 D.
D.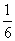
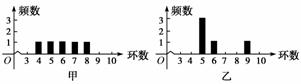
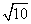 ,则|b|=( )
,则|b|=( )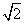 B.2
B.2 ,N=
,N= +
+ ,求M与N的大小关系.
,求M与N的大小关系.