题目内容
(本小题满分13分)
已知点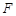 为抛物线
为抛物线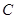 :
: 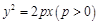 的焦点,
的焦点,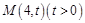 为抛物线
为抛物线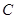 上的点,且
上的点,且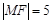 .
.
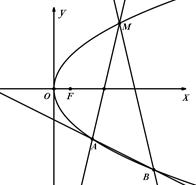
(Ⅰ)求抛物线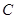 的方程和点
的方程和点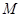 的坐标;
的坐标;
(Ⅱ)过点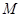 引出斜率分别为
引出斜率分别为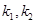 的两直线
的两直线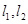 ,
, 与抛物线
与抛物线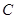 的另一交点为
的另一交点为 ,
,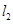 与抛物线
与抛物线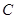 的另一交点为
的另一交点为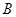 ,记直线
,记直线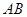 的斜率为
的斜率为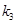 .
.
(ⅰ)若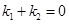 ,试求
,试求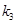 的值;
的值;
(ⅱ)证明: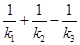 为定值.
为定值.
已知点
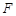 为抛物线
为抛物线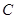 :
: 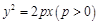 的焦点,
的焦点,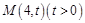 为抛物线
为抛物线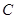 上的点,且
上的点,且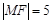 .
.
(Ⅰ)求抛物线
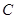 的方程和点
的方程和点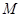 的坐标;
的坐标;(Ⅱ)过点
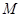 引出斜率分别为
引出斜率分别为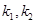 的两直线
的两直线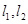 ,
, 与抛物线
与抛物线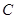 的另一交点为
的另一交点为 ,
,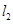 与抛物线
与抛物线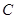 的另一交点为
的另一交点为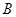 ,记直线
,记直线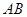 的斜率为
的斜率为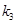 .
.(ⅰ)若
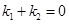 ,试求
,试求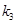 的值;
的值;(ⅱ)证明:
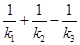 为定值.
为定值.(1)

(2) ,在第一问的基础上,分析得到三个斜率的关系式,然后化简变形得到证明。
,在第一问的基础上,分析得到三个斜率的关系式,然后化简变形得到证明。


(2)
 ,在第一问的基础上,分析得到三个斜率的关系式,然后化简变形得到证明。
,在第一问的基础上,分析得到三个斜率的关系式,然后化简变形得到证明。试题分析:解:(Ⅰ)∵
 ,∴
,∴
∴抛物线
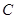 :
: .
.又
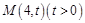 在抛物线
在抛物线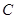 上,
上,∴
 .∴
.∴ .
.(Ⅱ)(ⅰ)设直线
 ,
,∵
 与抛物线
与抛物线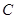 交于
交于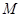 、
、 两点,∴
两点,∴ .
.由
 得:
得: ,
,设
 ,则
,则 ,
,∴
 ,即
,即 .
.同理可得
 .
. ,
, .
.∴
 .
.(ⅱ)证明:由(ⅰ)可知

 ,
, ,即证得
,即证得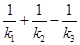 为定值.……13分
为定值.……13分点评:本题主要通过研究抛物线的标准方程、圆锥曲线的性质、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、数形结合思想、化归转化思想等

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
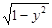 恰有一个公共点,则k的取值范围是___________
恰有一个公共点,则k的取值范围是___________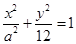 的一个焦点与抛物线
的一个焦点与抛物线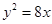 的焦点重合,则该椭圆的离心率为( )
的焦点重合,则该椭圆的离心率为( )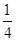
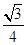
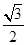
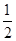

 与
与 轴交于点
轴交于点 ,与直线
,与直线
 交于点
交于点 ,椭圆
,椭圆 以
以 为右焦点,且过点
为右焦点,且过点 时,椭圆
时,椭圆



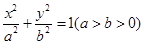 的两个焦点为
的两个焦点为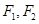 ,椭圆的离心率为
,椭圆的离心率为 ,
, 点是椭圆上任意一点, 且
点是椭圆上任意一点, 且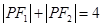 ,
,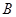 为直角顶点作椭圆的内接等腰直角三角形
为直角顶点作椭圆的内接等腰直角三角形 ,这样的等腰直角三角形是否存在?若存在请说明有几个、并求出直角边所在直线方程?若不存在,请说明理由.
,这样的等腰直角三角形是否存在?若存在请说明有几个、并求出直角边所在直线方程?若不存在,请说明理由.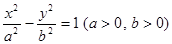 的左焦点
的左焦点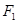 作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为A、B,若
作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为A、B,若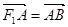 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )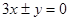 B.
B.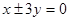
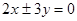 D.
D.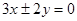
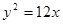 上,则这个三角形的面积为 。
上,则这个三角形的面积为 。 的一条渐近线方程为
的一条渐近线方程为 ,则其离心率为 。
,则其离心率为 。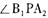 为钝角,则此椭圆的离心率的取值范围为
为钝角,则此椭圆的离心率的取值范围为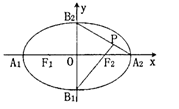
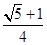 )
)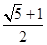 )
)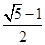 ,1)
,1)