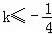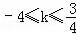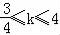题目内容
9.已知△ABC内接于圆O,且∠A=60°,若$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}(x、y∈R)$,则x+2y的最大值为( )| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | 2-$\frac{2\sqrt{2}}{3}$ |
分析 如图所示.过点O分别作OD⊥AB,OE⊥AC,其垂足分别为D,E,则D,E分别为弦AB,AC的中点.由∠BAC=60°,可得$\overrightarrow{AB}•\overrightarrow{AC}$=$\frac{1}{2}$bc.根据$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}(x、y∈R)$,可得$\overrightarrow{AO}$$•\overrightarrow{AB}$=x${\overrightarrow{AB}}^{2}$+y$\overrightarrow{AC}•\overrightarrow{AB}$,化为:$\frac{1}{2}{c}^{2}$=xc2+$\frac{1}{2}y$bc.由$\overrightarrow{AO}•\overrightarrow{AC}$=x$\overrightarrow{AB}•\overrightarrow{AC}$+y${\overrightarrow{AC}}^{2}$,化为:$\frac{1}{2}{b}^{2}$=$\frac{1}{2}$bcx+yb2.化简利用基本不等式的性质即可得出.
解答 解:如图所示.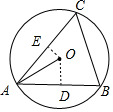
过点O分别作OD⊥AB,OE⊥AC,其垂足分别为D,E,
则D,E分别为弦AB,AC的中点.
∵∠BAC=60°,
∴$\overrightarrow{AB}•\overrightarrow{AC}$=$\frac{1}{2}$bc.
∵$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}(x、y∈R)$,
∴$\overrightarrow{AO}$$•\overrightarrow{AB}$=x${\overrightarrow{AB}}^{2}$+y$\overrightarrow{AC}•\overrightarrow{AB}$,化为:$\frac{1}{2}{c}^{2}$=xc2+$\frac{1}{2}y$bc,即c=2xc+yb.
$\overrightarrow{AO}•\overrightarrow{AC}$=x$\overrightarrow{AB}•\overrightarrow{AC}$+y${\overrightarrow{AC}}^{2}$,化为:$\frac{1}{2}{b}^{2}$=$\frac{1}{2}$bcx+yb2,即b=cx+2yb.
则x+2y=$\frac{2c-b}{3c}$+$\frac{4b-2c}{3b}$=2-$\frac{1}{3}$$(\frac{b}{c}+\frac{2c}{b})$≤2-$\frac{1}{3}$×$2\sqrt{\frac{b}{c}×\frac{2c}{b}}$=2-$\frac{2\sqrt{2}}{3}$.当且仅当b=$\sqrt{2}$c时取等号.
故选:D.
点评 本题考查了圆的性质、垂径定理、向量的数量积运算性质、基本不等式的性质,考查了推理能力与计算能力,属于难题.

| A. | $[{-\frac{3}{4},0}]$ | B. | $[{0,\frac{3}{4}}]$ | C. | $({-\frac{3}{4},0})$ | D. | $({0,\frac{3}{4}})$ |
| A. | a的最小值为-3 | B. | a的最小值为-4 | C. | a的最大值为2 | D. | a的最大值为4 |
 ,
, 求
求 和
和 的解析式.
的解析式.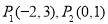 ,圆
,圆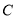 是以
是以 的中点为圆心,
的中点为圆心,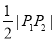 为半径的圆。
为半径的圆。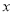 轴和
轴和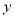 轴上截距相等,求切线方程;
轴上截距相等,求切线方程; 是圆
是圆 ,
,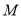 为切点,
为切点,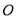 为坐标原点,且有
为坐标原点,且有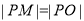 ,求使
,求使 最小的点
最小的点 的坐标.
的坐标. 或k≤﹣4
或k≤﹣4