题目内容
4.若某正棱台的底面是正方形,上底面边长为4cm,下底面边长为10cm,高为4cm,求此正棱台的全面积和体积.分析 先求出${S}_{1}={4}^{2}=16$,${S}_{2}=1{0}^{2}=100$,再求出斜率为5,此正棱台的全面积S=S1+S2+$\frac{上下底周长和}{2}$×斜高,体积V=$\frac{1}{3}({S}_{1}+{S}_{2}+\sqrt{{S}_{1}{S}_{2}})•h$,由此能求出结果.
解答 解:∵正棱台的底面是正方形,上底面边长为4cm,下底面边长为10cm,高为4cm,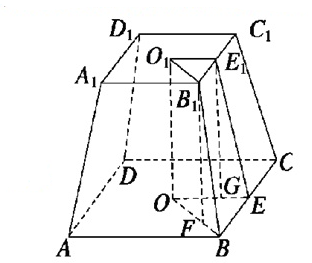
∴${S}_{1}={4}^{2}=16$,${S}_{2}=1{0}^{2}=100$,
如图,O1E1=OG=2,EG=OE-OG=5-2=3,
E1G=O1O=4,
∴E1E=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∴此正棱台的全面积S=S1+S2+$\frac{4×4+4×10}{2}×5$=16+100+140=256(cm2).
∴此正棱台体积V=$\frac{1}{3}({S}_{1}+{S}_{2}+\sqrt{{S}_{1}{S}_{2}})•h$
=$\frac{1}{3}(16+100+\sqrt{16×100})×4$=208(cm3).
点评 本题考查正四棱台的全面积和体积的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、空间想象能力、运算求解能力,考查函数与方程思想、化归与转化思想、数形结合思想,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知△ABC内接于圆O,且∠A=60°,若$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}(x、y∈R)$,则x+2y的最大值为( )
| A. | $\frac{2}{3}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | 2-$\frac{2\sqrt{2}}{3}$ |
13.已知向量$\overrightarrow{OA}=(1,-3),\overrightarrow{OB}=(2,-1),\overrightarrow{OC}=(k+1,k-2)$,若A、B、C三点共线,则实数k应满足的条件是( )
| A. | k=-2 | B. | $k=\frac{1}{2}$ | C. | k=1 | D. | k=-1 |
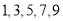 ,从这
,从这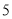 条线段中任取
条线段中任取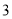 条,则所取
条,则所取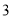 条线段能构成一个三角形的概率为
条线段能构成一个三角形的概率为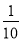 B.
B.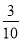 C.
C.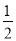 D.
D.
 与直线
与直线 相切于点
相切于点 ,则直线
,则直线 的方程为
的方程为 B.
B.
 D.
D.
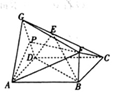 如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,∠GDC=90°,点E是线段GC上除两端点外的一点.
如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,∠GDC=90°,点E是线段GC上除两端点外的一点. 满足
满足 ,则
,则 的最大值为
的最大值为 B.
B. C.1 D.
C.1 D.