题目内容
(本小题满分14分)如图, 是边长为
是边长为 的正方形,
的正方形, 是矩形,平面
是矩形,平面 平面
平面 ,
, 为
为 的中点.
的中点.

(1)求证: //平面
//平面 ;
;
(2)若三棱锥 的体积为
的体积为 ,求二面角
,求二面角 的正切值.
的正切值.
(1)见解析;(2) 求二面角 的正切值为
的正切值为 .
.
【解析】
试题解析:(1) 连接 AE,设BF∩AE=O,连接OG,
∵四边形形 ABEF 是矩形,∴O为 AE的中点,
∵G 为EC的中点 ,∴OG 为△OAC 的中位线,
∴AC //OG 2分
∵OG 平面BFG, AC
平面BFG, AC 平面BFG
平面BFG
∴AC //平面BFG 4分
(2) 平面ABCD⊥平面ABEF,ABEF 是矩形,
∴BE⊥AB ,又平面ABCD∩平面ABEF=AB,
∴BE⊥面ABCD,同理可得BC⊥面ABEF 7 分
∵BC∩BE=B,∴AB⊥面BCE ,则三棱柱 AFD-BEC 是直三棱柱,
∴ DC⊥面BEC, DC 平面DCEF,
平面DCEF,
∴平面DCEF⊥平面BEC,又平面DCEF∩平面BEC=EC,
作BH⊥EC,垂足为H,则BH⊥平面DCEF, 9 分
设BE=a, ,
,
∴ ? 10分
? 10分
过点G 作GQ⊥BE ,垂足为Q,过点Q作QM⊥OE ,连接GM,
则∠GMQ为二面角E-BF-G的平面角 12分
又BC=BE=3,  ,∴
,∴ 14分
14分
向量法:平面ABCD⊥平面ABEF, ABEF是矩形,
∴BE⊥AB,又平面ABCD∩平面ABEF=AB,
∴BE⊥面ABCD,同理可得BC⊥面ABEF,
∵BC∩BE=B,∴AB⊥面BCE,则三棱柱AFD-BEC是直三棱柱,
∴AB,BE,BC两两垂直,故建立如图所示的空间直角坐标系: 9 分
则B(0,3,0),F(3,0,0),E(3,3,0), ,
,
∴ 10分
10分
设平面 的法向量为
的法向量为 ,由
,由 ,
,
得 ,取x=1,∴
,取x=1,∴ 12分
12分
又平面BFE 的一个法向量 13 分
13 分
∴ ,
,
∴所求二面角的平面角为锐角正切值为 14分
14分
考点:考查了线面平行的判定,求二面角.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案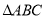 的重心为G,角A,B,C所对的边分别为
的重心为G,角A,B,C所对的边分别为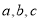 ,若
,若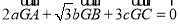 ,则
,则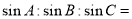
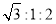 C.
C.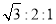 D.
D.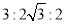
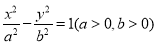 的右焦点
的右焦点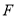 作垂直于
作垂直于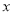 轴的直线,交双曲线的渐近线于
轴的直线,交双曲线的渐近线于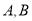 两点,若
两点,若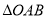 (
( 为坐标原点)是等边三角形,则双曲线的离心率为 ( )
为坐标原点)是等边三角形,则双曲线的离心率为 ( ) B.
B.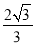 C.
C.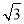 D.
D.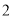
 为虚数单位,复数
为虚数单位,复数 ,
, =( )
=( ) C.
C. D.3
D.3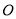 为顶点,边长为1的正方形
为顶点,边长为1的正方形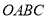 ,其中
,其中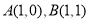 ,曲线
,曲线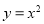 与
与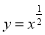 在正方形内围成一小片阴影,在正方形内任取一点
在正方形内围成一小片阴影,在正方形内任取一点 ,则点
,则点 取自阴影部分的概率为________.
取自阴影部分的概率为________. 的右焦点
的右焦点 作垂直于
作垂直于 轴的直线,交双曲线的渐近线于
轴的直线,交双曲线的渐近线于 两点,若
两点,若 (
( 为坐标原点)是等边三角形,则双曲线的离心率为 ( )
为坐标原点)是等边三角形,则双曲线的离心率为 ( ) B.
B. C.
C. D.
D.
 ,
, ,定义
,定义 ,其中
,其中 是
是 的共轭复数.对任意复数
的共轭复数.对任意复数 ,
, ,
, ,有如下四个命题:
,有如下四个命题: ;
; ;
; ;
; .
. B.
B. C.
C. D.
D.
 为奇函数,且在
为奇函数,且在 上是减函数,又
上是减函数,又  ,则
,则 的解集为( )
的解集为( )

