题目内容
17.已知函数f(x)=$sinx(cosx-\sqrt{3}sinx)$.(Ⅰ)求$f(\frac{π}{6})$的值;
(Ⅱ)求函数f(x)在区间[$0,\frac{π}{2}$]上的最值.
分析 (Ⅰ)先进行化简,利用代入法进行求解即可.
(Ⅱ)求出角的范围,结合三角函数的单调性进行求解即可.
解答 解:(Ⅰ)由题意可知,$f(x)=sinx•cosx-\sqrt{3}{sin^2}x$=$\frac{1}{2}sin2x-\frac{{\sqrt{3}(1-cos2x)}}{2}$…(2分)
=$\frac{1}{2}sin2x+\frac{{\sqrt{3}}}{2}cos2x-\frac{{\sqrt{3}}}{2}$=$sin(2x+\frac{π}{3})-\frac{{\sqrt{3}}}{2}$…(4分)
由此可知,$f(\frac{π}{6})=0$.…(6分)
(Ⅱ)由$0≤x≤\frac{π}{2}$可知,$\frac{π}{3}≤2x+\frac{π}{3}≤\frac{4π}{3}$,进而$-\frac{{\sqrt{3}}}{2}≤sin({2x+\frac{π}{3}})≤1$,…(8分)
当$0≤x≤\frac{π}{2}$时,$f(x)∈[-\sqrt{3},1-\frac{{\sqrt{3}}}{2}]$,…(9分)
所以函数f(x)在区间$[0,\frac{π}{2}]$上的最大值为$1-\frac{{\sqrt{3}}}{2}$,最小值为$-\sqrt{3}$. …(13分)
点评 本题主要考查三角函数的化简和求解,利用三角函数的图象和性质是解决本题的关键.

练习册系列答案
相关题目
18.设P为有公共焦点F1,F2的椭圆C1与双曲线C2的一个交点,且PF1⊥PF2,椭圆C1的离心率为e1,双曲线C2的离心率为e2,若3e1=e2,则e1=$\frac{\sqrt{5}}{3}$.
12.学校计划在周一至周四的艺术节上展演《雷雨》、《茶馆》、《天籁》和《马蹄声碎》四部话剧,每天一部.受多种因素影响,话剧《雷雨》不能在周一和周四上演;《茶馆》不能在周一和周三上演;《天籁》不能在周三和周四上演;《马蹄声碎》不能在周一和周四上演.那么下列说法正确的是( )
| A. | 《雷雨》只能在周二上演 | B. | 《茶馆》可能在周二或周四上演 | ||
| C. | 周三可能上演《雷雨》或《马蹄声碎》 | D. | 四部话剧都有可能在周二上演 |
6.下列函数,是偶函数,且周期为π的是( )
| A. | y=cos2x-sin2x | B. | y=sin2x+cos2x | C. | y=cos2x-sin2x | D. | y=sin2x+cosx |

 若某市6所中学参加中学生合唱比赛的得分用茎叶图表示如图,其中茎为十位数,叶为个位数,则这组数据的方差是$\frac{13}{3}$.
若某市6所中学参加中学生合唱比赛的得分用茎叶图表示如图,其中茎为十位数,叶为个位数,则这组数据的方差是$\frac{13}{3}$.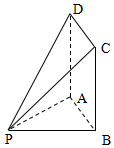 如图,四边形ABCD为矩形,PB=2,BC=3,PA⊥平面ABCD.
如图,四边形ABCD为矩形,PB=2,BC=3,PA⊥平面ABCD.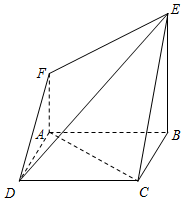 在如图所示的几何体中,四边形ABCD为正方形,四边形ABEF为直角梯形,且AF∥BE,AB⊥BE,平面ABCD∩平面ABEF=AB,AB=BE=2AF=2.
在如图所示的几何体中,四边形ABCD为正方形,四边形ABEF为直角梯形,且AF∥BE,AB⊥BE,平面ABCD∩平面ABEF=AB,AB=BE=2AF=2.