题目内容
已知f(x)=a2x-
ax(a>0,且a≠1)
(1)求f(x)的值域;
(2)解不等式f(x)>
.
| 1 |
| 2 |
(1)求f(x)的值域;
(2)解不等式f(x)>
| 1 |
| 2 |
考点:指、对数不等式的解法,函数的值域
专题:不等式的解法及应用
分析:(1)令ax=t(t>0)换元,得到关于t的一元二次函数后利用配方法求值域;
(2)求解关于ax的一元二次不等式,然后求解指数不等式得答案.
(2)求解关于ax的一元二次不等式,然后求解指数不等式得答案.
解答:
解:(1)令ax=t(t>0),
则f(x)=a2x-
ax=g(t)=t2-
t (t>0).
由g(t)=t2-
t=(t-
)2-
≥-
.
∴函数f(x)的值域为:[-
,+∞);
(2)由f(x)>
,得a2x-
ax>
.
即2(ax)2-ax-1>0,解得:ax<-
(舍)或ax>1.
由ax>1.
若a>1,解得:x>0;
若0<a<1,解得:x<0.
∴a>1时,不等式f(x)>
的解集为(0,+∞);
0<a<1时,不等式f(x)>
的解集为(-∞,0).
则f(x)=a2x-
| 1 |
| 2 |
| 1 |
| 2 |
由g(t)=t2-
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 16 |
∴函数f(x)的值域为:[-
| 1 |
| 16 |
(2)由f(x)>
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即2(ax)2-ax-1>0,解得:ax<-
| 1 |
| 2 |
由ax>1.
若a>1,解得:x>0;
若0<a<1,解得:x<0.
∴a>1时,不等式f(x)>
| 1 |
| 2 |
0<a<1时,不等式f(x)>
| 1 |
| 2 |
点评:本题考查了换元法,考查了利用配方法求函数的值域,训练了不等式的解法,是中档题.

练习册系列答案
相关题目
函数y=|1-x|的图象是( )
A、 |
B、 |
C、 |
D、 |
已知函数f(x)=
,则函数y=f[f(x)+1]的零点个数( )
|
| A、2 | B、3 | C、4 | D、5 |
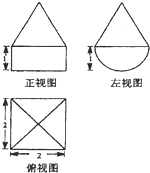 某几何体的三视图如图所示,其中正视图和左视图的上半部分均为边长为2的等边三角形,则该几何体的体积为( )
某几何体的三视图如图所示,其中正视图和左视图的上半部分均为边长为2的等边三角形,则该几何体的体积为( )A、π+
| ||||
B、2π+
| ||||
C、π+
| ||||
D、2π+
|