题目内容
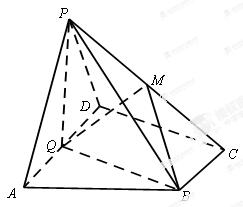
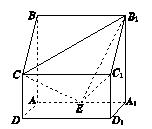
如图,在四棱锥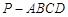 中,底面
中,底面 为直角梯形,
为直角梯形, ∥
∥ ,
,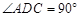 ,平面
,平面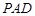 ⊥底面
⊥底面 ,
,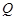 为
为 的中点,
的中点, 是棱
是棱 上的点,
上的点,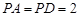 ,
,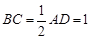 ,
,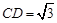 .
.
(Ⅰ)求证:平面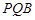 ⊥平面
⊥平面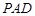 ;
;
(Ⅱ)若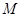 为棱
为棱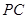 的中点,求异面直线
的中点,求异面直线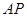 与
与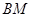 所成角的余弦值.
所成角的余弦值.
(Ⅰ)详见解析;(Ⅱ)异面直线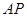 与
与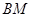 所成角的余弦值为
所成角的余弦值为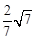
解析试题分析:(Ⅰ)证两平面垂直,先证一个面内的一条直线垂直另一个平面.
在本题中可证得: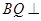 平面
平面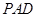 ,也可证:
,也可证: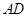 ⊥平面
⊥平面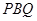 .
.
(Ⅱ)法一、由(Ⅰ)题可得:直线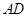 、
、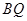 、
、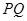 两两垂直,故可以
两两垂直,故可以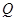 为原点建立空间直角坐标系,利用空间向量求异面直线
为原点建立空间直角坐标系,利用空间向量求异面直线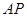 与
与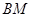 所成角的余弦值.
所成角的余弦值.
法二、可过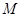 作
作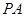 的平行线,从而将异面直线
的平行线,从而将异面直线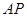 与
与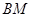 所成角转化相交直线所成的角.
所成角转化相交直线所成的角.
试题解析:(Ⅰ)法一: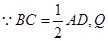 为
为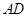 的中点,
的中点,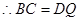
又 即
即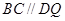
∴四边形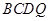 为平行四边形,
为平行四边形,

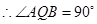 即
即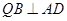
又∵平面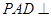 平面
平面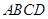 且平面
且平面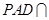 平面
平面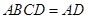
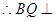 平面
平面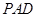
又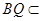 平面
平面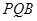 ,∴平面
,∴平面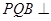 平面
平面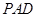 6分
6分
法二: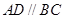 ,
,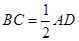 ,
,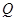 为
为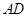 的中点,∴
的中点,∴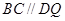 且
且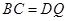 .
.
∴四边形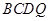 为平行四边形,∴
为平行四边形,∴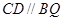
∵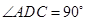 ∴
∴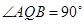 即
即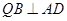
∵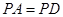 ∴
∴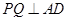
∵ 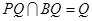 ,
,
∴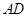 ⊥平面
⊥平面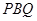 .
.
∵ 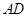
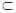 平面
平面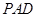 ,
,
∴平面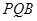 ⊥平面
⊥平面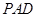 . 6分
. 6分
(Ⅱ)∵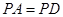 ,
,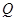 为
为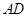 的中点,
的中点,
∴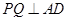 .
.
∵平面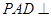 平面
平面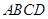 且平面
且平面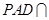 平面
平面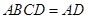
∴ 平面
平面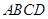 . 8分
. 8分
(注:不证明PQ⊥平面ABCD直接建系扣

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
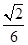 .求线段AM的长.
.求线段AM的长.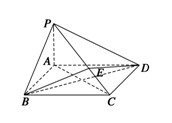
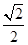 时,求四棱锥P-ABCD的外接球表面积.
时,求四棱锥P-ABCD的外接球表面积.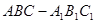 的侧面
的侧面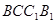 是菱形,
是菱形,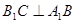 ,D是
,D是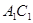 的中点,证明:
的中点,证明: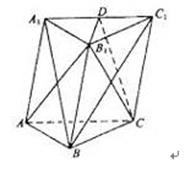
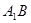 ∥面
∥面
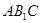
 平面
平面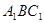 .
.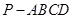 中,四边形
中,四边形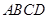 为矩形,
为矩形,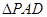 为等腰三角形,
为等腰三角形,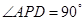 ,平面
,平面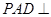 平面
平面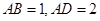 ,
,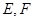 分别为
分别为 和
和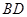 的中点.
的中点.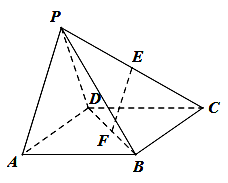
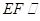 平面
平面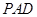 ;
;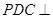 平面
平面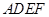 与梯形
与梯形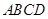 所在平面互相垂直,
所在平面互相垂直,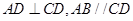 ,
,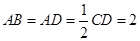 ,点
,点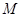 在线段
在线段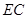 上且不与
上且不与 重合。
重合。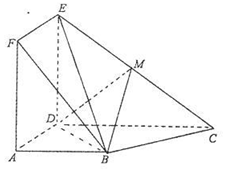
 时,求三棱锥
时,求三棱锥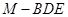 的体积.
的体积.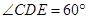 ,M是DE的中点,F是AC的中点,且AC=4,
,M是DE的中点,F是AC的中点,且AC=4,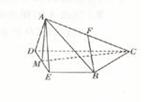
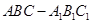 中,
中,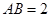 ,
,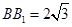 ,
, 为
为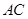 上的动点.
上的动点.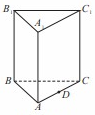
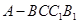 的体积;
的体积;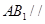 平面
平面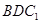 ,请说明理由;
,请说明理由;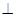 平面
平面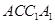 .
.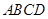 的边长为4,
的边长为4,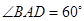 ,
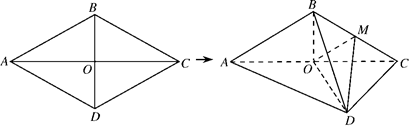
,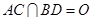 .将菱形
.将菱形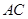 折起,得到三棱锥
折起,得到三棱锥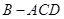 ,点
,点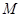 是棱
是棱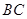 的中点,
的中点, .
.
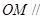 平面
平面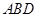 ;
;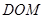
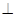 平面
平面 ;
; 的余弦值.
的余弦值.