Question

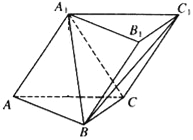
【题目】如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB交PB于点F．

（Ⅰ）证明 PA//平面EDB；

（Ⅱ）证明PB⊥平面EFD.

Answer 1

【答案】(Ⅰ)详见解析；(Ⅱ)详见解析.

【解析】

（I）连结，交于．连结，通过中位线证明，由此证得平面.（2）先证得平面，由此证得，而，故平面，由此证得，结合，可证得平面.

证明:（Ⅰ）连结，交于．连结．∵底面是正方形，∴点是的中点．在△中，是中位线，∴//．而平面，

且平面，所以，//平面．

（Ⅱ）∵⊥底面，且底面，∴⊥.

∵底面是正方形，有⊥,，平面，

平面,∴⊥平面．而平面，∴⊥.

又∵，是的中点，∴⊥，，

平面，平面.∴⊥平面．而平面，

∴⊥．又⊥，且，平面，

平面，所以⊥平面．