Question

【题目】已知函数.

（Ⅰ）当时，求曲线在点处的切线方程；

（Ⅱ）当时，证明： .

Answer 1

【答案】（1）（2）见解析

【解析】试题分析：（Ⅰ）先代入，对求导数，再算出， ，进而可得曲线在点处的切线方程；（Ⅱ）先构造函数，再利用导数可得的最小值，，进而可证当时， ．

试题解析：（Ⅰ）解：当时， ，

所以．

所以， .

所以曲线在点处的切线方程为．

即.

（Ⅱ）证法一：当时， .

要证明，只需证明.

以下给出三种思路证明.

思路1：设，则.

设，则，

所以函数 在上单调递增

因为， ，

所以函数在上有唯一零点，且

因为时，所以，即

当时， ；当时，

所以当时， 取得最小值．

故．

综上可知，当时， .

思路2：先证明 ．

设，则．

因为当时， ，当时， ，

所以当时，函数单调递减，当时，函数单调递增．

所以．

所以（当且仅当时取等号）．

所以要证明，

只需证明．

下面证明．

设，则．

当时， ，当时， ，

所以当时，函数单调递减，当时，函数单调递增．

所以．

所以（当且仅当时取等号）．

由于取等号的条件不同，

所以．

综上可知，当时， .

（若考生先放缩，或、同时放缩，请参考此思路给分！）

思路3：先证明.

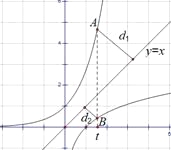
因为曲线与曲线的图像关于直线对称，

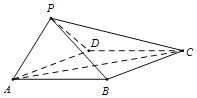
设直线 与曲线， 分别交于点， ，点， 到直线

的距离分别为， ，

则．

其中， ．

①设 ，则．

因为，所以．

所以在上单调递增，则．

所以．

②设 ，则．

因为当时， ；当时， ，

所以当时， 单调递减；当时， 单调递增．

所以．

所以．

所以．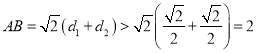

综上可知，当时， .

证法二：因为，

要证明，只需证明.

以下给出两种思路证明.

思路1：设，则.

设，则．

所以函数 在上单调递增．

因为， ，

所以函数在上有唯一零点，且.

因为，所以，即．

当时， ；当时， .

所以当时， 取得最小值．

故．

综上可知，当时， ．

思路2：先证明，且．

设，则．

因为当时， ；当时， ，

所以在上单调递减，在上单调递增．

所以当时， 取得最小值．

所以，即（当且仅当时取等号）．

由，得（当且仅当时取等号）．

所以（当且仅当时取等号）．

再证明．

因为， ，且与不同时取等号，

所以 ．

综上可知，当时， ．