题目内容
在某校组织的一次篮球定点投篮训练中,规定每人最多投3次. 在A处每投进一球得3分;在B处每投进一球得2分. 如果前两次得分之和超过3分就停止投篮;否则投第三次. 某
同学在A处的投中率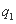 为0.25,在B处的投中率为
为0.25,在B处的投中率为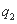 . 该同学选择先在A处投一球,以后都在B处投,用
. 该同学选择先在A处投一球,以后都在B处投,用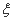 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Ⅰ)求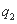 的值;
的值;
(Ⅱ)求随机变量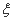 的数学期望E
的数学期望E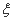 ;
;
(Ⅲ)试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分
的概率的大小.
解:(Ⅰ)
设该同学在A处投中为事件A, 在B处投中为事件B.
则事件A,B相互独立,且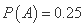 ,
,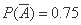 ,
,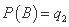 ,
,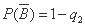 .
.
根据分布列知: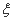 =0时,
=0时,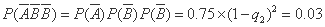 ,
,
所以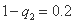 ,
,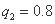 . … 2分
. … 2分
(Ⅱ)
当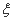 =2时,
=2时,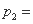
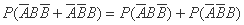
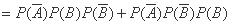
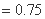
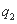 (
( 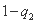 )
)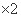
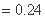 . … 4分
. … 4分
当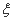 =3时,
=3时,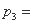
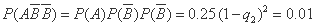 . … 6分
. … 6分
当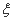 = 4时,
= 4时,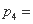
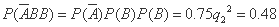 . … 8分
. … 8分
当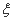 = 5时,
= 5时,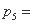
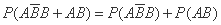
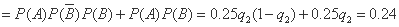 . … 10分
. … 10分
所以随机变量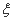 的分布列为w.w.w.k.s.5.u.c.o.m
的分布列为w.w.w.k.s.5.u.c.o.m
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∴随机变量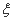 的数学期望
的数学期望
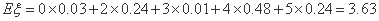 . … 11分
. … 11分
(Ⅲ)
该同学选择都在B处投篮得分超过3分的概率为
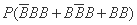
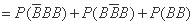
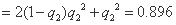 . … 13分
. … 13分
该同学选择(1)中方式投篮得分超过3分的概率为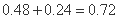 . … 14分
. … 14分
由此看来该同学选择都在B处投篮得分超过3分的概率大. … 14分

设全集 集合
集合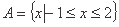 ,
,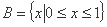 ,则
,则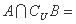 ( )
( )
| (A) | (B) |
| (C) | (D) |
设集合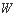 由满足下列两个条件的数列
由满足下列两个条件的数列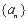 构成:
构成:
①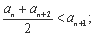 ②存在实数
②存在实数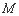 ,使
,使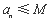 .(
.(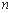 为正整数).在以下数列
为正整数).在以下数列
⑴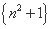 ;(2)
;(2) ; (3)
; (3)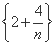 ;(4)
;(4)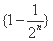
中属于集合W的数列编号为 ( )
| (A)(1)(2) | (B)(3) (4) | (C)(2)(3) | (D)(2) (4) |
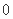
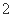


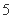
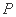
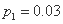

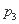
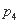
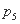
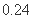
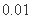
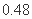
 是递增数列;
是递增数列;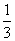 ,2]都有|f(x)|≤1成立,则a的取值范围是________.
,2]都有|f(x)|≤1成立,则a的取值范围是________. 的图象向右平移
的图象向右平移 个单位,再将图象上每一点的
个单位,再将图象上每一点的 倍(纵坐标不变),所得图象关于直线
倍(纵坐标不变),所得图象关于直线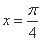 对称,则
对称,则 的最小
的最小 B.
B.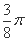 C.
C. D.
D.
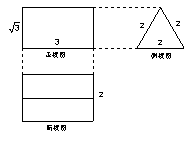 右图是一个几何体的三视图,已知侧视图是一个
右图是一个几何体的三视图,已知侧视图是一个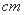 ),
),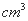 ;
;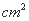 .
. 


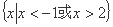
 ,现已进入药物临床试用阶段,每个试用组由4位该病毒的感染者组成,其中2人试用甲种抗病毒药物,2人试用乙种抗病毒药物,如果试用组中,甲种抗病毒药物治愈人数人数超过乙种抗病毒药物的治愈人数,则称该组为“甲类组”,
,现已进入药物临床试用阶段,每个试用组由4位该病毒的感染者组成,其中2人试用甲种抗病毒药物,2人试用乙种抗病毒药物,如果试用组中,甲种抗病毒药物治愈人数人数超过乙种抗病毒药物的治愈人数,则称该组为“甲类组”, 表示这3个试用组中“甲类组”的个数,求
表示这3个试用组中“甲类组”的个数,求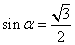 是
是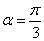 的( )
的( )