题目内容
(本小题满分13分)
如图6,平行四边形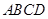 中,
中,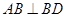 ,
,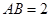 ,
,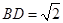 ,沿
,沿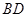 将
将 折
折
起,使二面角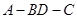 是大小为锐角
是大小为锐角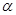 的二面角,设
的二面角,设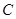 在平面
在平面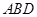 上的射影为
上的射影为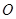 .
.
(1)当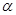 为何值时,三棱锥
为何值时,三棱锥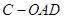 的体积最大?最大值为多少?
的体积最大?最大值为多少?
(2)当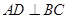 时,求
时,求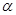 的大小.
的大小.
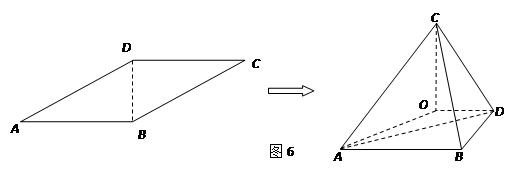
如图6,平行四边形
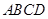 中,
中,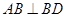 ,
,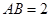 ,
,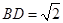 ,沿
,沿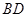 将
将 折
折起,使二面角
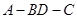 是大小为锐角
是大小为锐角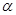 的二面角,设
的二面角,设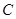 在平面
在平面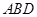 上的射影为
上的射影为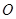 .
.(1)当
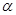 为何值时,三棱锥
为何值时,三棱锥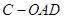 的体积最大?最大值为多少?
的体积最大?最大值为多少?(2)当
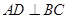 时,求
时,求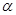 的大小.
的大小.
解:(1)由题知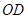 为
为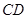 在平面
在平面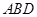 上的射影,
上的射影,
∵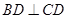 ,
, 平面
平面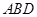 ,∴
,∴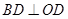 ,
,
∴ , ………………………2分
, ………………………2分
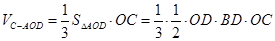
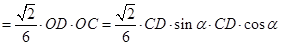 ………………4分
………………4分

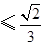 , ……………………5分
, ……………………5分
当且仅当 ,即
,即 时取等号,
时取等号,
∴当 时,三棱锥
时,三棱锥 的体积最大,最大值为
的体积最大,最大值为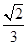 . …………6分
. …………6分

(2)(法一)连接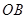 , ……………………7分
, ……………………7分
∵ 平面
平面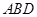 ,
,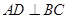 ,
,
∴ 平面
平面 ,
,
∴ , ………………………9分
, ………………………9分
∴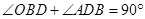 ,
,
故 ,
,
∴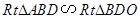 , ………………11分
, ………………11分
∴ ,
,

∴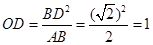 , …………………………………………………12分
, …………………………………………………12分
在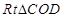 中,
中, ,得
,得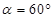 .…………………13分
.…………………13分
(法二) 过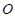 作
作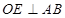 于
于 ,则
,则 为矩形,
为矩形,
以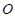 为原点,
为原点,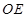 ,
, ,
,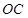 所在直线分别为
所在直线分别为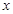 轴、
轴、
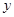 轴、
轴、 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,
则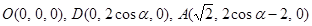 ,
,
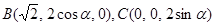 , ………9分
, ………9分
于是 ,
,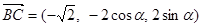 , ……………10分
, ……………10分
由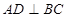 ,得
,得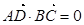 ,
,
∴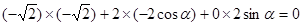 , ……………………12分
, ……………………12分
得 ,又
,又 为锐角,∴
为锐角,∴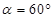 . ………………………………13分
. ………………………………13分
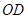 为
为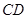 在平面
在平面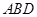 上的射影,
上的射影,∵
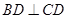 ,
, 平面
平面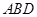 ,∴
,∴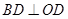 ,
,∴
 , ………………………2分
, ………………………2分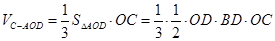
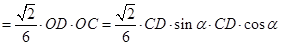 ………………4分
………………4分
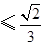 , ……………………5分
, ……………………5分当且仅当
 ,即
,即 时取等号,
时取等号,∴当
 时,三棱锥
时,三棱锥 的体积最大,最大值为
的体积最大,最大值为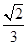 . …………6分
. …………6分
(2)(法一)连接
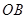 , ……………………7分
, ……………………7分∵
 平面
平面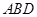 ,
,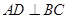 ,
,∴
 平面
平面 ,
,∴
 , ………………………9分
, ………………………9分∴
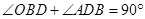 ,
,故
 ,
,∴
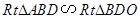 , ………………11分
, ………………11分∴
 ,
,
∴
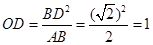 , …………………………………………………12分
, …………………………………………………12分在
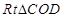 中,
中, ,得
,得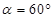 .…………………13分
.…………………13分(法二) 过
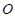 作
作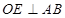 于
于 ,则
,则 为矩形,
为矩形,以
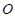 为原点,
为原点,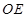 ,
, ,
,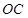 所在直线分别为
所在直线分别为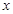 轴、
轴、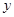 轴、
轴、 轴,建立如图所示的空间直角坐标系,
轴,建立如图所示的空间直角坐标系,则
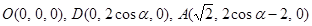 ,
,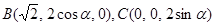 , ………9分
, ………9分于是
 ,
,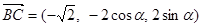 , ……………10分
, ……………10分由
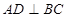 ,得
,得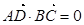 ,
,∴
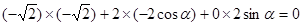 , ……………………12分
, ……………………12分得
 ,又
,又 为锐角,∴
为锐角,∴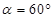 . ………………………………13分
. ………………………………13分略

练习册系列答案
相关题目
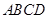 中,
中,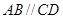 ,
,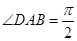 ,点
,点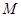 、
、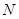 分别在
分别在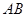 ,
,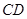 上,且
上,且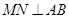 ,
,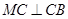 ,
, ,
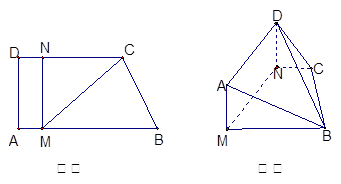
,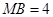 ,现将梯形
,现将梯形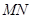 折起,使平面
折起,使平面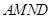 与平面
与平面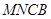 垂直(如图乙).
垂直(如图乙).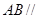 平面
平面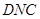 ;
; 的长为何值时,二面角
的长为何值时,二面角 的大小为
的大小为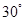 ?
?
 中,点
中,点 分别在棱
分别在棱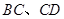 上,满足
上,满足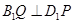 ,
,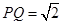 .
.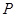 、
、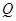 两点的位置.
两点的位置.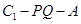 大小的余弦值.
大小的余弦值.
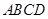 中,
中,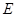 是
是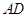 中点,
中点,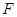 是
是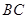 中点,
中点,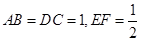 ,则直
,则直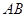 与
与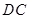 所成的角大小为( )
所成的角大小为( )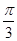
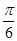
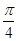
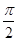
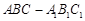 ,
,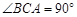 ,
,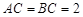 ,
,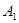 在底面
在底面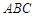 上的射影恰为
上的射影恰为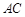 的中点
的中点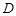 ,又知
,又知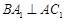 .
.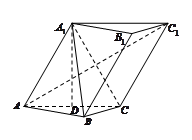
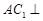 平面
平面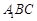 ;
; 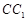 到平面
到平面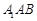 的距离;
的距离;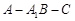 的大小。
的大小。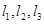 是空间三条不同的直线,则下列命题正确的是( )
是空间三条不同的直线,则下列命题正确的是( )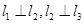 ,则
,则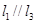
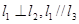 ,则
,则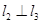
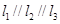 ,则
,则 与
与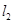 相交,
相交,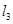 相交,则
相交,则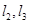 共面
共面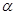 、
、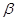 是两个不同的平面,给出下列四个命题.
是两个不同的平面,给出下列四个命题.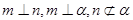 ,则
,则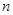 ∥
∥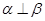 ,
,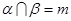 ,
,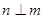 ,则
,则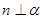 或
或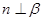 ;
;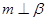 ,
,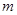 ∥
∥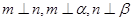 ,则
,则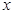 的圆柱.
的圆柱.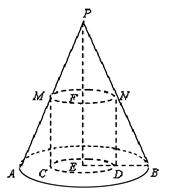
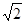 的四棱锥
的四棱锥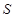 -
- 的底面是边长为1的正方形,点
的底面是边长为1的正方形,点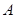 、
、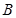 、
、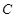 、
、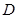 均在半径为1的同一球面上,则底面
均在半径为1的同一球面上,则底面