题目内容
8.己知A(1,0,0),B(0,1,0),C(0,0,1),则平面ABC的一个单位法向量是$(\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3})$.分析 设平面ABC的一个法向量为$\overrightarrow{n}$=(x,y,z),可得$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=0}\\{\overrightarrow{n}•\overrightarrow{AC}=0}\end{array}\right.$,即可得出平面ABC的一个单位法向量=$\frac{\overrightarrow{n}}{|\overrightarrow{n}|}$.
解答 解:$\overrightarrow{AB}$=(-1,1,0),$\overrightarrow{AC}$=(-1,0,1),
设平面ABC的一个法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=0}\\{\overrightarrow{n}•\overrightarrow{AC}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{-x+y=0}\\{-x+z=0}\end{array}\right.$,取$\overrightarrow{n}$=(1,1,1).
则平面ABC的一个单位法向量=$\frac{\overrightarrow{n}}{|\overrightarrow{n}|}$=$(\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3})$.
故答案为:$(\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3},\frac{\sqrt{3}}{3})$.
点评 本题考查了平面法向量的应用、数量积运算性质,考查了推理能力与计算能力,属于基础题.

 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
| A. | 若 m∥α,n∥α,则 m∥n | B. | 若 m⊥α,n?α,则 m⊥n | ||
| C. | 若 m⊥α,m⊥n,则 n∥α | D. | 若 m∥α,m⊥n,则 n⊥α |
| A. | 0 | B. | $\frac{686}{3}$ | C. | $\frac{49π}{2}$ | D. | 49π |
| 交强险浮动因素和浮动费率比率表 | ||
| 浮动因素 | 浮动比率 | |
| A1 | 上一个年度未发生有责任道路交通事故 | 下浮10% |
| A2 | 上两个年度未发生有责任道路交通事故 | 下浮20% |
| A3 | 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| A4 | 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| A5 | 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| A6 | 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
| 类型 | A1 | A2 | A3 | A4 | A5 | A6 |
| 数量 | 10 | 5 | 5 | 20 | 15 | 5 |
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的概率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有6辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选两辆车,求这两车辆中恰好有一辆事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌的二手车,求一辆车盈利的平均值.
| A. | $3\sqrt{3}$ | B. | $2\sqrt{7}$ | C. | $\frac{20}{3}$ | D. | $\frac{17}{3}$ |
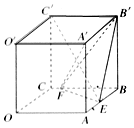 如图,在棱长为2的正方体OABC-O′A′B′C′中,E,F分别是棱AB,BC上的动点.
如图,在棱长为2的正方体OABC-O′A′B′C′中,E,F分别是棱AB,BC上的动点.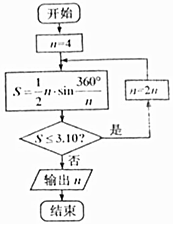 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( )(参考数据:sin22.5°=0.3827,sin11.25°=0.1951,sin5.625°=0.0980)
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为( )(参考数据:sin22.5°=0.3827,sin11.25°=0.1951,sin5.625°=0.0980)