Question

【题目】已知数列的前项和为，且.

（1）证明是等比数列，并求的通项公式；

（2）求；

（3）设,若对恒成立，求实数的取值范围.

Answer 1

【答案】（1）； （2）； （3）.

【解析】

（1）设，将已知条件中的式子进行转化，可得，从而证得其为等比数列，之后利用等比数列的通项公式求得，进而求得；

（2）利用错位相减法对数列求和，求得；

（3）根据题意求得，将恒成立转化为，利用作差比较法，求得，观察得出，进而求得的范围.

（1）设，则只需证明为等比数列即可，

因为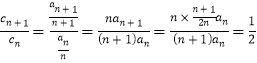为常数，

所以数列是公比为的等比数列，且首项，

则，所以.

（2）由（1）知 ①

②

①-②得，

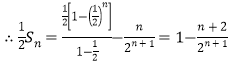
（3）由（2）得，，

要使得对恒成立，只需，

因为，

所以，当时，，即，

当时，，即，所以，

所以.