题目内容
【题目】设a+b=2，b＞0，则当a=时， 
取得最小值．
【答案】﹣2
【解析】解：∵a+b=2，b＞0，
∴ 
= 
，（a＜2）
设f（a）= ，（a＜2），画出此函数的图象，如图所示．
利用导数研究其单调性得，
当a＜0时，f（a）=﹣ 
+ 
，
f′（a）= 
= 
，当a＜﹣2时，f′（a）＜0，当﹣2＜a＜0时，f′（a）＞0，
故函数在（﹣∞，﹣2）上是减函数，在（﹣2，0）上是增函数，
∴当a=﹣2时， 取得最小值 
．
同样地，当0＜a＜2时，得到当a= 
时， 取得最小值 
．
综合，则当a=﹣2时， 取得最小值．
所以答案是：﹣2．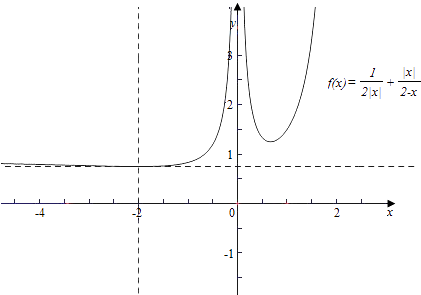
【考点精析】通过灵活运用基本不等式，掌握基本不等式：
,（当且仅当
时取到等号）；变形公式：
即可以解答此题．
练习册系列答案
相关题目
