题目内容
3.设公差为d(d为奇数,且d>1)的等差数列{an}的前n项和为Sn,若Sm-1=-9,Sm=0,其中m>3,且m∈N*,则an=3n-12.分析 Sm-1=-9,Sm=0,其中m>3,可得:(m-1)a1+$\frac{(m-1)(m-2)}{2}$d=-9,ma1+$\frac{m(m-1)}{2}$d=0,化为:d=$\frac{18}{m-1}$.由于m>3,且m∈N*,d为奇数,且d>1,通过分类讨论验证即可得出.
解答 解:∵Sm-1=-9,Sm=0,其中m>3,
∴(m-1)a1+$\frac{(m-1)(m-2)}{2}$d=-9,
ma1+$\frac{m(m-1)}{2}$d=0,
可得:d=$\frac{18}{m-1}$.
∵m>3,且m∈N*,d为奇数,且d>1,
∴d=3,m=7.
∴a1=-9.
∴an=-9+3(n-1)=3n-12.
故答案为:3n-12.
点评 本题考查了等差数列的通项公式及其前n项和公式,考查了分类讨论、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
11.已知x,y满足约束条件$\left\{\begin{array}{l}x+y-3≥0\\ y-2x+6≥0\\ y-\frac{1}{2}x≤0\end{array}\right.$,则z=x-y的最小值为( )
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
8.已知0≤x$≤\frac{π}{2}$,函数y=sinx+cosx的最大值、最小值分别为( )
| A. | $\sqrt{2}$,-$\sqrt{2}$ | B. | $\sqrt{2}$,1 | C. | $\sqrt{2}$,0 | D. | 2,-2 |
15.设a>0,则${∫}_{-a}^{a}$$\frac{xdx}{1+cosx}$=( )
| A. | 1 | B. | 0 | C. | 2a | D. | $\frac{3}{4}$a |
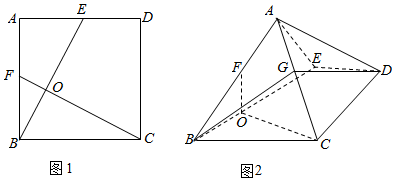 如图1已知正方形ABCD的边长为2,E,F分别为边AD、AB的中点,将△ABE沿BE折起,使平面ABE⊥平面BCDE,如图2,点G为AC的中点
如图1已知正方形ABCD的边长为2,E,F分别为边AD、AB的中点,将△ABE沿BE折起,使平面ABE⊥平面BCDE,如图2,点G为AC的中点