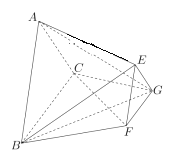
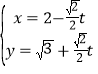题目内容
【题目】在棱长为1的正方体
中，点
是对角线
上的动点（点与
不重合），则下列结论正确的是____.
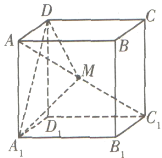
①存在点，使得平面
平面
；
②存在点，使得
平面
；
③
的面积不可能等于
；
④若
分别是
在平面
与平面
的正投影的面积，则存在点，使得
.
【答案】①②④
【解析】
逐项分析.
①如图
当
是
中点时，可知也是
中点且
，
，
，所以
平面
，所以
，同理可知
，且
，所以
平面
，又
平面
，所以平面
平面，故正确；
②如图
取靠近
的一个三等分点记为，记
，
，因为
，所以
，所以
为靠近
的一个三等分点，则为
中点，又
为
中点，所以
，且
，
，
，所以平面
平面
，且
平面，所以
平面，故正确；
③如图
作
，在
中根据等面积得：
，根据对称性可知：
，又
，所以
是等腰三角形，则
，故错误；
④如图
设
，
在平面
内的正投影为
，在平面
内的正投影为
，所以
，
，当
时，解得：
，故正确.
故填：①②④.
练习册系列答案
阅读快车系列答案
相关题目
