Question

【题目】如图，在四棱锥中，底面是直角梯形，且，．

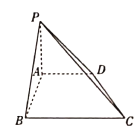
（1）证明：平面；

（2）求平面与平面所成锐二面角的余弦值．

Answer 1

【答案】（1）证明见解析；（2）.

【解析】

（1）推导出PA⊥AD，PA⊥AB，由此能证明PA⊥平面ABCD．（2）以A为原点，AB，AD，AP为x，y，z轴的正方向建立空间直角坐标系，利用向量法能求出平面PBC与平面PAD所成锐二面角的余弦值．

(1)因为,所以,即.

同理可得.

因为.所以平面.

(2)由题意可知,两两垂直,故以A为原点,分别为轴的正方向建立如图所示的空间直角坐标系,

则，

所以.

设平面的法向量为，

则，

不妨取则

易得平面,所以平面的一个法向量为，

记平面与平面所成锐二面角为,则

故平面与平面所成锐二面角的余弦值为.