Question

【题目】已知椭圆的离心率为，分别为左，右焦点，分别为左，右顶点，原点到直线的距离为.设点在第一象限，且轴，连接交椭圆于点.

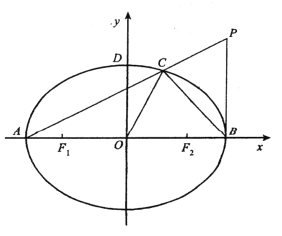
（1）求椭圆的方程；

（2）若三角形的面积等于四边形的面积，求直线的方程；

（3）求过点的圆方程（结果用表示）.

Answer 1

【答案】（1）.（2）.（3） .

【解析】试题分析：（1）由离心率为，得，，利用 两点坐标可得的方程为，由圆心到时直线的距离公式求得，则.（2）设，，由 两点的坐标可得直线 的方程，与椭圆的方程联立可得 的坐标（ 的横、纵坐标分别是 的高），代入三角形的面积公式结合面积相等的条件即得关于 的方程求出 ，最后再将代入PA方程即可得所求. （3）所求圆的圆心为 的垂直平分线的交点，利用 三点的坐标即可得的垂直平分线的方程，两个方程联立即可求得圆心的坐标，再代入圆的标准方程即可得所求.

试题解析：

（1）因为椭圆的，

所以，，

所以直线的方程为，

又到直线的距离为，所以，

所以，，

所以椭圆的方程为.

（2）设，，

直线的方程为，

由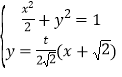，整理得，

解得：，则点的坐标是，

因为三角形的面积等于四边形的面积，所以三角形的面积等于三角形的面积，

，

，

则，解得.

所以直线的方程为.

（3）因为，，，

所以的垂直平分线，

的垂直平分线为，

所以过三点的圆的圆心为，

则过三点的圆方程为 ，

即所求圆方程为 .