题目内容
已知圆C: 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线 交圆C于A、B两点。
交圆C于A、B两点。
(1)当 经过圆心C时,求直线
经过圆心C时,求直线 的方程;
的方程;
(2)当弦AB的长为 时,写出直线
时,写出直线 的方程。
的方程。
(1) (2)
(2) 或
或
解析试题分析:(1)圆心坐标为(1,0), ,
, ,整理得
,整理得 。
。
(2)圆的半径为3,当直线l的斜率存在时,设直线l的方程为 ,整理得
,整理得 ,圆心到直线l的距离为
,圆心到直线l的距离为 ,
,
解得 ,代入整理得
,代入整理得 。
。
当直线l的斜率不存在时,直线l的方程为 ,经检验符合题意。
,经检验符合题意。 直线l的方程为
直线l的方程为 或
或 。
。
考点:直线方程及直线与圆的位置关系
点评:当直线与圆相交时,圆的半径,圆心到直线的距离以及弦长的一半构成直角三角形,此直角三角形的求解计算是经常用到的

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 外切于点
外切于点 ,且半径为
,且半径为 的圆的方程.
的圆的方程.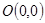 的圆C与直线
的圆C与直线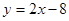 相切于点
相切于点 .
. 的坐标为
的坐标为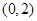 ,设
,设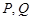 分别是直线
分别是直线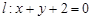 和圆
和圆 上的动点,求
上的动点,求 的最小值.
的最小值. 关于直线
关于直线 对称,且以
对称,且以 为直径的圆经过原点?若存在,写出直线
为直径的圆经过原点?若存在,写出直线 是圆
是圆 上的动点,
上的动点, 的取值范围;
的取值范围; 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线 交圆C于A、B两点。
交圆C于A、B两点。 时,写出直线
时,写出直线 ,直线
,直线 :
: .
. 时,求直线
时,求直线 、
、 是单位圆
是单位圆 上的点,
上的点, 是圆与
是圆与 轴正半轴的交点,三角形
轴正半轴的交点,三角形 为正三角形, 且AB∥
为正三角形, 且AB∥
 的三个三角函数值;
的三个三角函数值; 及
及 .
.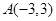 发出的光线
发出的光线 射到
射到 轴上,被
轴上,被 相切,求光线
相切,求光线 中,设二次函数
中,设二次函数 的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求:
的图象与两坐标轴有三个交点,经过这三个交点的圆记为C.求: