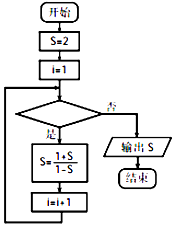
题目内容
【题目】如图，已知点P（2，0），且正方形ABCD内接于⊙O：x2+y2=1，M、N分别为边AB、BC的中点．当正方形ABCD绕圆心O旋转时， 
的取值范围为 ． 
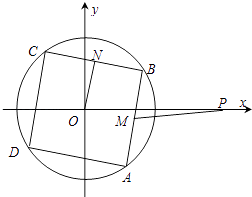
【答案】[﹣ 
， ]
【解析】解：设M（ 
cosα， sinα）， ∵ 
⊥ 
，
∴ =0，
∴N（﹣ sinα， cosα），
∴ =（﹣ sinα， cosα）， =（ cosα， sinα），
∴ 
=（ cosα﹣2， sinα），
∴ =﹣ sinα（ cosα﹣2）+ 
sinαcosα
= sinα，
∵sinα∈[﹣1，1]，
∴ sinα∈[﹣ 
， ]，
∴ 的取值范围是[﹣ ， ]．
所以答案是：[﹣ ， ]．
练习册系列答案
相关题目
【题目】随着人口老龄化的到来，我国的劳动力人口在不断减少，”延迟退休“已经成为人们越来越关注的话题，为了解公众对“延迟退休”的态度，某校课外研究性学习小组在某社区随机抽取了50人进行调查，将调查情况进行整理后制成下表：
年龄 | [20，25） | [25，30） | [30，35） | [35，40） | [40，45） |
人数 | 4 | 5 | 8 | 5 | 3 |
年龄 | [45，50） | [50，55） | [55，60） | [60，65） | [65，70） |
人数 | 6 | 7 | 3 | 5 | 4 |
经调查年龄在[25，30），[55，60）的被调查者中赞成人数分别是3人和2人，现从这两组的被调查者中各随机选取2人，进行跟踪调查．
（Ⅰ）求年龄在[25，30）的被调查者中选取的2人都赞成“延迟退休”的概率；
（Ⅱ）若选中的4人中，不赞成“延迟退休”的人数为X，求随机变量X的分布列和数学期望．
