题目内容
【题目】已知函数f(x)=4x﹣2x , 实数s,t满足f(s)+f(t)=0,a=2s+2t , b=2s+t .
(1)当函数f(x)的定义域为[﹣1,1]时,求f(x)的值域;
(2)求函数关系式b=g(a),并求函数g(a)的定义域D;
(3)在(2)的结论中,对任意x1∈D,都存在x2∈[﹣1,1],使得g(x1)=f(x2)+m成立,求实数m的取值范围.
【答案】
(1)解:∵函数f(x)=4x﹣2x,f(x)的定义域为[﹣1,1]时,
∴t=2x∈[ ![]() ,2],g(t)=t2﹣t单调递增,
,2],g(t)=t2﹣t单调递增,
∵g( ![]() )=﹣
)=﹣ ![]() ,g(2)=2,
,g(2)=2,
∴f(x)的值域为:[﹣ ![]() ,2].
,2].
(2)解:∵f(s)+f(t)=0,
∴4s﹣2s+4t﹣2t=0,
化简得出:(2s+2t)2﹣22s+t﹣(2s+2t)=0,
∵a=2s+2t,b=2s+t.2s+2t≥2 ![]() .a≥2
.a≥2 ![]()
∴a2﹣2b﹣a=0,a≥2 ![]() ,a≥2
,a≥2 ![]() ,a>0
,a>0
即b= ![]() ,1<a≤2,D=(1,2];
,1<a≤2,D=(1,2];
(3)解:g(x)= ![]() (x2﹣x)∈(0,1],f(x)∈[﹣
(x2﹣x)∈(0,1],f(x)∈[﹣ ![]() ,2].
,2].
∵对任意x1∈D,都存在x2∈[﹣1,1],使得g(x1)=f(x2)+m成立,
∴(0,1][﹣ ![]() +m,2+m].
+m,2+m].
∴﹣1≤m≤ ![]() .
.
【解析】(1)换元根据t=2x∈[ ![]() ,2],g(t)=t2﹣t单调递增,即可求f(x)的值域;(2)配方得出:(2s+2t)2﹣22s+t﹣(2s+2t)=0,a2﹣2b﹣a=0,a≥2
,2],g(t)=t2﹣t单调递增,即可求f(x)的值域;(2)配方得出:(2s+2t)2﹣22s+t﹣(2s+2t)=0,a2﹣2b﹣a=0,a≥2 ![]() ,a≥2
,a≥2 ![]() ,a>0,求解即可得出b=
,a>0,求解即可得出b= ![]() ,1<a≤2;(3)g(x)=
,1<a≤2;(3)g(x)= ![]() (x2﹣x)∈(0,1],f(x)∈[﹣
(x2﹣x)∈(0,1],f(x)∈[﹣ ![]() ,2],对任意x1∈D,都存在x2∈[﹣1,1],使得g(x1)=f(x2)+m成立,即可求实数m的取值范围.
,2],对任意x1∈D,都存在x2∈[﹣1,1],使得g(x1)=f(x2)+m成立,即可求实数m的取值范围.
【考点精析】解答此题的关键在于理解函数的最值及其几何意义的相关知识,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值,以及对二次函数的性质的理解,了解当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
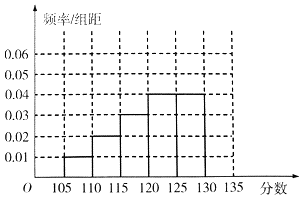
小学生10分钟应用题系列答案【题目】某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
组数 | 分组 | 19题满分人数 | 19题满分人数占本组人数比例 |
第一组 | [105,110] | 15 | 0.3 |
第二组 | [110,115) | 30 | 0.3 |
第三组 | [115,120) | x | 0.4 |
第四组 | [120,125) | 100 | 0.5 |
第五组 | [125,130) | 120 | 0.6 |
第六组 | [130,135) | 195 | y |
(Ⅰ)补全所给的频率分布直方图,并求n,x,y的值;
(Ⅱ)现从[110,115)、[115,120)两个分数段的19题满分的试卷中,按分层抽样的方法抽取9份进行展出,并从9份试卷中选出两份作为优秀试卷,优秀试卷在[115,120)中的分数记为ξ,求随机变量ξ的分布列及期望.