题目内容
8.在梯形ABCD中,已知AB∥CD,AB=2CD=2,$\frac{\overrightarrow{AD}}{|\overrightarrow{AD}|}•\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$=$\frac{1}{2}$,动点E和F分别在线段CD和BC上,且$\overrightarrow{BA}•\overrightarrow{BE}$的最大值为$\frac{7}{2}$,则$\overrightarrow{AC}•\overrightarrow{AF}$的取值范围为[$\frac{7}{4}$,$\frac{5}{2}$].分析 根据数量积的几何意义,可知,当点E在D处时,$\overrightarrow{BA}•\overrightarrow{BE}$最大,过D、C分别作AB的垂线,垂足为M、N.则$\overrightarrow{BA}•\overrightarrow{BE}$的最大值为BA•BM=$\frac{7}{2}$,得BM,AM,BN.根据数量积的几何意义,可知,当点F在C处时,$\overrightarrow{AC}•\overrightarrow{AF}$最小,此时$\overrightarrow{AC}•\overrightarrow{AF}$=$\overrightarrow{AC}•\overrightarrow{AC}=\frac{7}{4}$,当点F在B处时,$\overrightarrow{AC}•\overrightarrow{AF}$最大,此时$\overrightarrow{AC}•\overrightarrow{AF}$=$\overrightarrow{AC}•\overrightarrow{AB}=AB•AN=\frac{5}{2}$.
解答 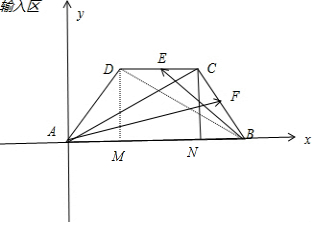 解:由$\frac{\overrightarrow{AD}}{|\overrightarrow{AD}|}•\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$=$\frac{1}{2}$,得∠DAC=60°.
解:由$\frac{\overrightarrow{AD}}{|\overrightarrow{AD}|}•\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$=$\frac{1}{2}$,得∠DAC=60°.
根据数量积的几何意义,可知,当点E在D处时,$\overrightarrow{BA}•\overrightarrow{BE}$最大,
过D、C分别作AB的垂线,垂足为M、N
则$\overrightarrow{BA}•\overrightarrow{BE}$的最大值为BA•BM=$\frac{7}{2}$,∴BM=$\frac{7}{4}$,
⇒AM=$\frac{1}{4}$,BN=$\frac{3}{4}$
以A为原点,ADF方向为x轴,建立平面直角坐标系,如图所示,
则A(0,0),B(2,0),C($\frac{5}{4},\frac{\sqrt{3}}{4}$),D($\frac{1}{4},\frac{\sqrt{3}}{4}$)
根据数量积的几何意义,可知,当点F在C处时,$\overrightarrow{AC}•\overrightarrow{AF}$最小,此时$\overrightarrow{AC}•\overrightarrow{AF}$=$\overrightarrow{AC}•\overrightarrow{AC}=\frac{7}{4}$.
当点F在B处时,$\overrightarrow{AC}•\overrightarrow{AF}$最大,此时$\overrightarrow{AC}•\overrightarrow{AF}$=$\overrightarrow{AC}•\overrightarrow{AB}=AB•AN=\frac{5}{2}$.
∴则$\overrightarrow{AC}•\overrightarrow{AF}$的取值范围为[$\frac{7}{4},\frac{5}{2}$]
故答案为:[$\frac{7}{4},\frac{5}{2}$]
点评 本题主要考查两个向量数量积运算,特别是几何意义,属于中档题.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案| A. | 2.2 | B. | 2.4 | C. | 2.6 | D. | 2.8 |
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
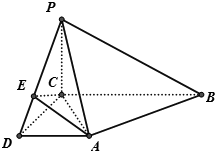 如图,在四棱锥P-ABCD中,AD∥BC,且BC=2,AD=CD=PC=1,AD⊥CD,PC⊥平面ABCD,点E在棱PD上,且PE=2ED.
如图,在四棱锥P-ABCD中,AD∥BC,且BC=2,AD=CD=PC=1,AD⊥CD,PC⊥平面ABCD,点E在棱PD上,且PE=2ED.