题目内容
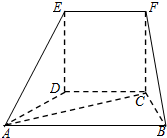 在如图的几何体中,平面CDEF为正方形,平面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.
在如图的几何体中,平面CDEF为正方形,平面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.(1)求证:AC⊥平面FBC;
(2)求直线BF与平面ADE所成角的正弦值.
分析:(1)证明1:由余弦定理得AC=
BC,所以AC⊥BC,由此能够证明AC⊥平面FBC.
证明2:设∠BAC=α,∠ACB=120°-α.由正弦定理能推出AC⊥BC,由此能证明AC⊥平面FBC.
(2)解法1:由(1)结合已知条件推导出AC⊥FC.由平面CDEF为正方形,得到CD⊥FC,由此入手能求出直线BF与平面ADE所成角的正弦值.
解法2:由题设条件推导出CA,CB,CF两两互相垂直,建立空间直角坐标系利用向量法能求出直线BF与平面ADE所成角的正弦值.
| 3 |
证明2:设∠BAC=α,∠ACB=120°-α.由正弦定理能推出AC⊥BC,由此能证明AC⊥平面FBC.
(2)解法1:由(1)结合已知条件推导出AC⊥FC.由平面CDEF为正方形,得到CD⊥FC,由此入手能求出直线BF与平面ADE所成角的正弦值.
解法2:由题设条件推导出CA,CB,CF两两互相垂直,建立空间直角坐标系利用向量法能求出直线BF与平面ADE所成角的正弦值.
解答:(1)证明1:因为AB=2BC,∠ABC=60°,
在△ABC中,由余弦定理得:
AC2=(2BC)2+BC2-2×2BC•BC•cos60°,
即AC=
BC.…(2分)
所以AC2+BC2=AB2.
所以AC⊥BC.…(3分)
因为AC⊥FB,BF∩BC=B,BF、BC?平面FBC,
所以AC⊥平面FBC.…(4分)
证明2:因为∠ABC=60°,
设∠BAC=α(0°<α<120°),则∠ACB=120°-α.
在△ABC中,由正弦定理,得
=
.…(1分)
因为AB=2BC,所以sin(120°-α)=2sinα.
整理得tanα=
,所以α=30°.…(2分)
所以AC⊥BC.…(3分)
因为AC⊥FB,BF∩BC=B,BF、BC?平面FBC,
所以AC⊥平面FBC.…(4分)
(2)解法1:由(1)知,AC⊥平面FBC,FC?平面FBC,
所以AC⊥FC.
因为平面CDEF为正方形,所以CD⊥FC.
因为AC∩CD=C,所以FC⊥平面ABCD.…(6分)
取AB的中点M,连结MD,ME,
因为ABCD是等腰梯形,且AB=2BC,∠DAM=60°,
所以MD=MA=AD.所以△MAD是等边三角形,且ME∥BF.…(7分)
取AD的中点N,连结MN,NE,则MN⊥AD.…(8分)
因为MN?平面ABCD,ED∥FC,所以ED⊥MN.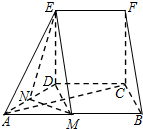
因为AD∩ED=D,所以MN⊥平面ADE. …(9分)
所以∠MEN为直线BF与平面ADE所成角. …(10分)
因为NE?平面ADE,所以MN⊥NE.…(11分)
因为MN=
AD,ME=
=
AD,…(12分)
在Rt△MNE中,sin∠MEN=
=
.…(13分)
所以直线BF与平面ADE所成角的正弦值为
.…(14分)
解法2:由(1)知,AC⊥平面FBC,FC?平面FBC,
所以AC⊥FC.
因为平面CDEF为正方形,所以CD⊥FC.
因为AC∩CD=C,所以FC⊥平面ABCD.…(6分)
所以CA,CB,CF两两互相垂直,
建立如图的空间直角坐标系C-xyz.…(7分)
因为ABCD是等腰梯形,且AB=2BC,∠ABC=60°
所以CB=CD=CF.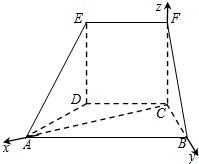
不妨设BC=1,则B(0,1,0),F(0,0,1),A(
,0,0),D(
,-
,0),E(
,-
,1),
所以
=(0,-1,1),
=(
,
,0),
=(0,0,1).…(9分)
设平面ADE的法向量为
=(x,y,z),
则有
即
取x=1,得
=(1,-
,0)是平面ADE的一个法向量.…(11分)
设直线BF与平面ADE所成的角为θ,
则sinθ=|cos?
,
>|=|
|=|
|=
.…(13分)
所以直线BF与平面ADE所成角的正弦值为
.…(14分)
在△ABC中,由余弦定理得:
AC2=(2BC)2+BC2-2×2BC•BC•cos60°,
即AC=
| 3 |
所以AC2+BC2=AB2.
所以AC⊥BC.…(3分)
因为AC⊥FB,BF∩BC=B,BF、BC?平面FBC,
所以AC⊥平面FBC.…(4分)
证明2:因为∠ABC=60°,
设∠BAC=α(0°<α<120°),则∠ACB=120°-α.
在△ABC中,由正弦定理,得
| BC |
| sinα |
| AB |
| sin(120°-α) |
因为AB=2BC,所以sin(120°-α)=2sinα.
整理得tanα=
| ||
| 3 |
所以AC⊥BC.…(3分)
因为AC⊥FB,BF∩BC=B,BF、BC?平面FBC,
所以AC⊥平面FBC.…(4分)
(2)解法1:由(1)知,AC⊥平面FBC,FC?平面FBC,
所以AC⊥FC.
因为平面CDEF为正方形,所以CD⊥FC.
因为AC∩CD=C,所以FC⊥平面ABCD.…(6分)
取AB的中点M,连结MD,ME,
因为ABCD是等腰梯形,且AB=2BC,∠DAM=60°,
所以MD=MA=AD.所以△MAD是等边三角形,且ME∥BF.…(7分)
取AD的中点N,连结MN,NE,则MN⊥AD.…(8分)
因为MN?平面ABCD,ED∥FC,所以ED⊥MN.

因为AD∩ED=D,所以MN⊥平面ADE. …(9分)
所以∠MEN为直线BF与平面ADE所成角. …(10分)
因为NE?平面ADE,所以MN⊥NE.…(11分)
因为MN=
| ||
| 2 |
| MD2+DE2 |
| 2 |
在Rt△MNE中,sin∠MEN=
| MN |
| ME |
| ||
| 4 |
所以直线BF与平面ADE所成角的正弦值为
| ||
| 4 |
解法2:由(1)知,AC⊥平面FBC,FC?平面FBC,
所以AC⊥FC.
因为平面CDEF为正方形,所以CD⊥FC.
因为AC∩CD=C,所以FC⊥平面ABCD.…(6分)
所以CA,CB,CF两两互相垂直,
建立如图的空间直角坐标系C-xyz.…(7分)
因为ABCD是等腰梯形,且AB=2BC,∠ABC=60°
所以CB=CD=CF.

不妨设BC=1,则B(0,1,0),F(0,0,1),A(
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
所以
| BF |
| DA |
| ||
| 2 |
| 1 |
| 2 |
| DE |
设平面ADE的法向量为
| n |
则有
|
|
取x=1,得
| n |
| 3 |
设直线BF与平面ADE所成的角为θ,
则sinθ=|cos?
| BF |
| n |
| ||||
|
|
(0,-1,1)•(1,-
| ||
|
| ||
| 4 |
所以直线BF与平面ADE所成角的正弦值为
| ||
| 4 |
点评:本题考查直线与平面垂直的证明,考查直线与平面所成角的正弦值,解题时要注意向量法的合理运用,注意空间思维能力的培养.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
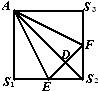 19、如图在正方形AS1S2S3中,E、F分别是边S1S2、S2S3的中点,D是EF的中点,沿AE、EF、AF把这个正方形折成一个几何体,使三点S1、S2、S3重合于一点S,下面有5个结论:
19、如图在正方形AS1S2S3中,E、F分别是边S1S2、S2S3的中点,D是EF的中点,沿AE、EF、AF把这个正方形折成一个几何体,使三点S1、S2、S3重合于一点S,下面有5个结论: (2013•上海) 在xOy平面上,将两个半圆弧(x-1)2+y2=1(x≥1)和(x-3)2+y2=1(x≥3),两条直线y=1和y=-1围成的封闭图形记为D,如图中阴影部分,记D绕y轴旋转一周而成的几何体为Ω.过(0,y)(|y|≤1)作Ω的水平截面,所得截面积为4π
(2013•上海) 在xOy平面上,将两个半圆弧(x-1)2+y2=1(x≥1)和(x-3)2+y2=1(x≥3),两条直线y=1和y=-1围成的封闭图形记为D,如图中阴影部分,记D绕y轴旋转一周而成的几何体为Ω.过(0,y)(|y|≤1)作Ω的水平截面,所得截面积为4π 平面上,将两个半圆弧
平面上,将两个半圆弧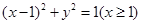 和
和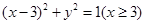 、两条直线
、两条直线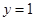 和
和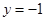 围成的封闭图形记为D,如图中阴影部分.记D绕y轴旋转一周而成的几何体为
围成的封闭图形记为D,如图中阴影部分.记D绕y轴旋转一周而成的几何体为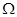 ,过
,过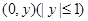 作
作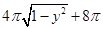 ,试利用祖暅原理、一个平放的圆柱和一个长方体,得出
,试利用祖暅原理、一个平放的圆柱和一个长方体,得出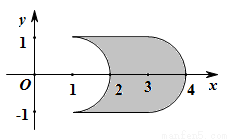

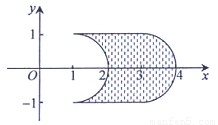 在xOy平面上,将两个半圆弧(x-1)2+y2=1(x≥1)和(x-3)2+y2=1(x≥3),两条直线y=1和y=-1围成的封闭图形记为D,如图中阴影部分,记D绕y轴旋转一周而成的几何体为Ω.过(0,y)(|y|≤1)作Ω的水平截面,所得截面积为4π
在xOy平面上,将两个半圆弧(x-1)2+y2=1(x≥1)和(x-3)2+y2=1(x≥3),两条直线y=1和y=-1围成的封闭图形记为D,如图中阴影部分,记D绕y轴旋转一周而成的几何体为Ω.过(0,y)(|y|≤1)作Ω的水平截面,所得截面积为4π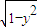 +8π.试利用祖恒原理、一个平放的圆柱和一个长方体,得出Ω的体积值为 .
+8π.试利用祖恒原理、一个平放的圆柱和一个长方体,得出Ω的体积值为 .