题目内容
在某次抽奖活动中,一个口袋里装有4个白球和4个黑球,所有球除颜色外无任何不同,每次从中摸出2个球,观察颜色后放回,若为同色,则中奖.
(1)求仅一次摸球中奖的概率;
(2)求连续2次摸球,恰有一次不中奖的概率;
(3)记连续3次摸球中奖的次数为ξ,求ξ的分布列和数学期望.
(1)求仅一次摸球中奖的概率;
(2)求连续2次摸球,恰有一次不中奖的概率;
(3)记连续3次摸球中奖的次数为ξ,求ξ的分布列和数学期望.
(1)设仅一次摸球中奖的概率为P1,则P1=
=
…(3分)
(2)设连续2次摸球(每次摸后放回),恰有一次不中奖的概率为P2,则
P2=
(1-P1)P1=
…(7分)
(3)ξ的取值可以是0,1,2,3,
P(ξ=0)=(1-P1)3=
,
P(ξ=1)=
(1-P1)2P1=
,
P(ξ=2)=
(1-P1)P12=
,
P(ξ=3)=
=
所以ξ的分布列如下表
…(12分)
∴Eξ=0•
+1•
+2•
+3•
=
….(14分)
2
| ||
|
| 3 |
| 7 |
(2)设连续2次摸球(每次摸后放回),恰有一次不中奖的概率为P2,则
P2=
| C | 12 |
| 24 |
| 49 |
(3)ξ的取值可以是0,1,2,3,
P(ξ=0)=(1-P1)3=
| 64 |
| 343 |
P(ξ=1)=
| C | 13 |
| 144 |
| 343 |
P(ξ=2)=
| C | 23 |
| 108 |
| 343 |
P(ξ=3)=
| P | 31 |
| 27 |
| 343 |
所以ξ的分布列如下表
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
∴Eξ=0•
| 64 |
| 343 |
| 144 |
| 343 |
| 108 |
| 343 |
| 27 |
| 343 |
| 441 |
| 343 |

练习册系列答案
相关题目
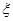 ,求
,求