题目内容
13.解关于x的不等式x2+ax-(a+1)<0.分析 根据题意,讨论a的取值范围,求出不等式x2+ax-(a+1)<0的解集即可.
解答 解:∵不等式x2+ax-(a+1)<0中,
△=a2+4(a+1)=(a+2)2≥0,
∴不等式x2+ax-(a+1)=0的两个实数根为1和-a-1;
当1=-a-1时,a=-2,不等式x2+ax-(a+1)<0无解;
当1>-a-1时,a>-2,不等式x2+ax-(a+1)<0的解集为{x|-a-1<x<1};
当1<-a-1时,a<-2,不等式x2+ax-(a+1)<0的解集为{x|1<x<-a-1};
综上,a=-2时,不等式x2+ax-(a+1)<0的解集为∅;
a>-2时,不等式x2+ax-(a+1)<0的解集为{x|-a-1<x<1};
a<-2时,不等式x2+ax-(a+1)<0的解集为{x|1<x<-a-1}.
点评 本题考查了含有字母系数的不等式的解法与应用问题,解题时应对字母系数进行讨论,是基础题目.

练习册系列答案
相关题目
3.($\frac{2}{x}$+x)(1-$\sqrt{x}$)4的展开式中x的系数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 12 |
8.下列函数中,与函数f(x)=$\frac{{2}^{x}-{2}^{-x}}{{2}^{x}+{2}^{-x}}$的单调性与奇偶性都相同的是( )
| A. | y=sinx | B. | y=x3-x | C. | y=2x | D. | y=lg(x+$\sqrt{{x}^{2}+1}$) |
18.为了了解汽车在某一路段上的速度,交警对这段路上连续驶过的50辆汽车的速度(单位:km/h)进行了统计,得到的数据如下表所示:
(1)试估计这段路上汽车行驶的平均速度;
(2)试估计在这段路上,汽车行驶速度的标准差.(注:为了计算方便,速度取每个区间的中点)
| 速度区间 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) | [100,110) |
| 车辆数 | 1 | 4 | 10 | 15 | 12 | 6 | 2 |
(2)试估计在这段路上,汽车行驶速度的标准差.(注:为了计算方便,速度取每个区间的中点)
5.y=cosx的图象相当于y=sinx的图象向左移动( )
| A. | 2π | B. | π | C. | $\frac{3π}{2}$ | D. | $\frac{π}{2}$ |
2.已知2α是第四象限角,且sinαtanα<0,则α在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
 如图,在△ABC中,点D在边BC上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{\sqrt{2}}{10}$
如图,在△ABC中,点D在边BC上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{\sqrt{2}}{10}$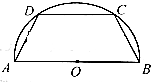 如图,有一块半径为R的半圆形钢板,计划将其剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.
如图,有一块半径为R的半圆形钢板,计划将其剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.