题目内容
(本小题满分12分)已知函数 ,函数
,函数 的最小值为
的最小值为 .
.
(1)求 ;
;
(2)是否存在实数m,n同时满足下列条件:
①
②当 的定义域为
的定义域为 时,值域为
时,值域为 ?若存在,求出m,n的值;若不存在,说明理由.
?若存在,求出m,n的值;若不存在,说明理由.
(1) ;(2)不存在这样的m,n.
;(2)不存在这样的m,n.
【解析】
试题分析:(1)一个是用换元法简化关系,注意t的取值范围 ,再借助二次函数的单调情况分三种情况讨论何时取到最小值,
,再借助二次函数的单调情况分三种情况讨论何时取到最小值,
当 时,
时,
当 时,
时,
当 时,
时, ,
,
从而得到 ;
;
(2)因为
 在
在 上是减函数,
上是减函数, ,无解.
,无解.
试题解析:(1)因为 ,所以
,所以
设 ,则
,则
当 时,
时,
当 时,
时,
当 时,
时,

(2)假设满足题意的m,n存在, 因为
 在
在 上是减函数,
上是减函数,
 因为
因为 的定义域为[n,m],值域为 [n2 ,m2],
的定义域为[n,m],值域为 [n2 ,m2],
 ,相减得6(m-n)=(m-n)(m+n)
,相减得6(m-n)=(m-n)(m+n)
由 所以m+n=6但这与
所以m+n=6但这与 矛盾
矛盾
所以满足题意的m,n不存在.
考点:分段函数的解析式,定义域,值域,最值.

练习册系列答案
相关题目
 ,
, ,
, ,由
,由 的大小关系为( )
的大小关系为( )  B.
B. C.
C. D.
D.
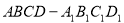 中,PQ是异面直线
中,PQ是异面直线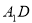 与AC的公垂线,则直线PQ与
与AC的公垂线,则直线PQ与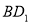 的位置关系为( )
的位置关系为( )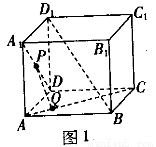
 与
与 的等比中项为 .
的等比中项为 . ,则△ABC一定是
,则△ABC一定是 的增区间是____________.
的增区间是____________. ,且
,且 ,则函数
,则函数 与函数
与函数 的图像可能是( )
的图像可能是( )
 的焦点为顶点,顶点为中心,离心率为2的双曲线方程是 __ .
的焦点为顶点,顶点为中心,离心率为2的双曲线方程是 __ .  中,
中, .
. ,F为PC的中点,
,F为PC的中点, .
.
 的长:
的长: 的正弦值.
的正弦值.