题目内容
20.已知x.y,z均为实数,且a=x2-y一z+$\frac{π}{2}$,b=y2-x-z+$\frac{π}{3}$,c=z2-x-y+$\frac{π}{4}$,求证:a,b,c中最多有两个小于或等于0.分析 假设a,b,c均小于或等于0,由条件和不等式的性质可以推出矛盾,可得假设不正确,从而命题得证.
解答 证明:假设a,b,c均小于或等于0,即x2-y一z+$\frac{π}{2}$≤0,y2-x-z+$\frac{π}{3}$≤0,z2-x-y+$\frac{π}{4}$≤0,…(4分)
由不等式的可加性得:x2-y-z+$\frac{π}{2}$+y2-x-z+$\frac{π}{3}$+z2-x-y+$\frac{π}{4}$≤0,…(8分)
即(x-1)2+(y-1)2+(z-1)2+$\frac{13}{12}π$-3≤0,…(10分)
这显然不成立,故假设不正确,所以,a、b、c中最多有两个小于或等于0. …(12分)
点评 本题主要考查用反证法证明数学命题,推出矛盾,是解题的关键和难点,属于中档题.

练习册系列答案
相关题目
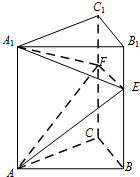 如图,正三棱柱ABC-A1B1C1中,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,则三棱锥A-A1EF的体积是8$\sqrt{3}$.
如图,正三棱柱ABC-A1B1C1中,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,则三棱锥A-A1EF的体积是8$\sqrt{3}$.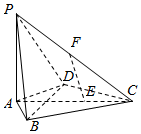 在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点.
在四棱锥P-ABCD中,PA⊥底面ABCD,AB=AD=2,CB=CD=$\sqrt{7}$,∠BAD=120°,点E在线段AC上,且AE=2EC,F为线段PC的中点.