题目内容
已知函数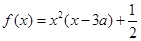 ,
,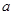 为实数,(
为实数,( ).
).
(Ⅰ)若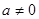 ,求函数
,求函数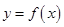 的极值;
的极值;
(Ⅱ)若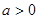 ,且函数
,且函数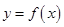 有三个不同的零点,求实数
有三个不同的零点,求实数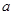 的取值范围.
的取值范围.
【答案】
当 .
……2分
.
……2分
令 ,得
,得 ,或
,或 .
.
且 ,
,
 .
……4分
.
……4分
(Ⅰ)(1)当 时,
时, .
.
当 变化时,
变化时, 、
、 的变化情况如下表:
的变化情况如下表:
|
|
|
0 |
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
↗ |
|
↘ |
|
↗ |
∴ 当 时,在
时,在 处,函数
处,函数 有极大值
有极大值 ;在
;在 处,函数
处,函数 有极小值
有极小值 . ……8分
. ……8分
(2)当a < 0时,2a < 0.
当 变化时,
变化时, 、
、 的变化情况如下表:
的变化情况如下表:
|
|
|
2a |
|
0 |
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
↗ |
|
↘ |
|
↗ |
∴ 当a<0时,在x=2a处,函数 有极大值
有极大值 ;在x=0处,函数
;在x=0处,函数 有极小值
有极小值 .
……12分
.
……12分
(Ⅱ)要使函数 有三个不同的零点,
有三个不同的零点,
必须 .
解得
.
解得 .
.
∴当 时,函数
时,函数 有三个不同的零点. ……14分
有三个不同的零点. ……14分
【解析】略

练习册系列答案
相关题目









 (
( 为实数).
为实数). 时,
求
时,
求 的最小值;
的最小值; 上是单调函数,求
上是单调函数,求 (
( 为实数).
为实数). 时,
求
时,
求 的最小值;
的最小值; 上是单调函数,求
上是单调函数,求 (
( 为实数,
为实数,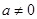 ,
, ).
). 的图像过点
的图像过点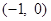 ,且方程
,且方程 有且只有一个根,求
有且只有一个根,求 当
当 ,
, ,
, ,且函数
,且函数 能否大于
能否大于 ?
?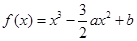 (
( 为实数,且
为实数,且 ),在区间
),在区间 上最大值为
上最大值为 ,最小值为
,最小值为
 的解析式
的解析式 在区间
在区间 上为减函数,求实数
上为减函数,求实数 的取值范围
的取值范围 作函数
作函数 图象的切线,求切线方程
图象的切线,求切线方程