题目内容
(文)(本小题14分)已知函数 (
( 为实数).
为实数).
(1)当 时,
求
时,
求 的最小值;
的最小值;
(2)若 在
在 上是单调函数,求
上是单调函数,求 的取值范围.
的取值范围.
【答案】
(1)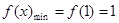 ;(2)
;(2) .
.
【解析】本试题主要考查了导数在研究函数中的运用。第一问中利用当a=0时, ,对于x分类讨论,当
,对于x分类讨论,当 时,
时,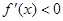 当
当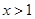 时,
时,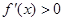 ,故
,故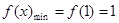
第二问中,由
① 由题意可知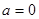 时,
时,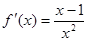 ,在
,在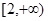 时,
时,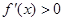 符合要求
符合要求
② 当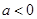 时,令
时,令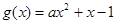
故此时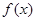 在
在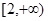 上只能是单调递减
上只能是单调递减
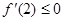 即
即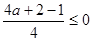 解得
解得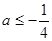
当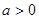 时,
时,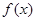 在
在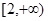 上只能是单调递增
上只能是单调递增
 即
即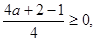 得
得
综上可得结论。
(Ⅰ) 由题意可知: …..1分
…..1分
当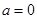 时
时 ..…. 2分
..…. 2分
当 时,
时,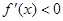 当
当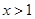 时,
时,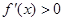 ………..4分
………..4分
故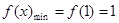 .
…...6分
.
…...6分
(Ⅱ) 由
① 由题意可知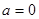 时,
时,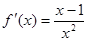 ,在
,在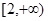 时,
时,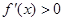 符合要求 ………..8分
符合要求 ………..8分
② 当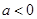 时,令
时,令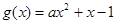
故此时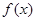 在
在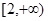 上只能是单调递减
上只能是单调递减
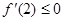 即
即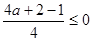 解得
解得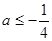 ………….10分
………….10分
当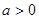 时,
时,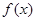 在
在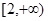 上只能是单调递增
上只能是单调递增
 即
即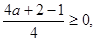 得
得
故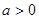 ……...12分
……...12分
综上 …………...14分
…………...14分

练习册系列答案
相关题目
 如图,已知圆
如图,已知圆