题目内容
有如下几种说法：
①若直线l1，l2的斜率存在且相等，则l1∥l2；
②若直线l1⊥l2，则它们的斜率之积为-1；
③若两条直线的倾斜角的正弦值相等，则这两条直线平行．
在以上三种说法中，正确的个数是（ ）
①若直线l1，l2的斜率存在且相等，则l1∥l2；
②若直线l1⊥l2，则它们的斜率之积为-1；
③若两条直线的倾斜角的正弦值相等，则这两条直线平行．
在以上三种说法中，正确的个数是（ ）
| A、1 | B、2 | C、3 | D、0 |
考点：命题的真假判断与应用
专题：直线与圆,简易逻辑
分析：根据直线斜率相等，直线平行或重合，可判断①，根据两条直线的斜率一个为0一个不存在时，两直线也垂直，可判断②；根据两条直线的倾斜角的正弦值相等，则他们的倾斜角相等或互补，可判断③．
解答：
解：对于①，若直线l1，l2的斜率存在且相等，则l1与l2平行或重合，故①错误；
对于②，若直线l1⊥l2，则它们的斜率之积为-1，或一个为0一个不存在，故②错误；
对于③，若两条直线的倾斜角的正弦值相等，则他们的倾斜角相等或互补，则这两条直线不一定平行，故③错误．
故正确命题的个数有0个，
故选：D．
对于②，若直线l1⊥l2，则它们的斜率之积为-1，或一个为0一个不存在，故②错误；
对于③，若两条直线的倾斜角的正弦值相等，则他们的倾斜角相等或互补，则这两条直线不一定平行，故③错误．
故正确命题的个数有0个，
故选：D．
点评：本题以命题的真假判断为载体，考查了直线斜率的几何意义，直线垂直的充要条件，直线倾斜角的几何意义等知识点，难度不大，属于基础题．
练习册系列答案
相关题目
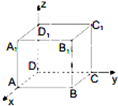如图，把棱长为2的正方体ABCD-A1B1C1D1放在空间直角坐标系中，使D与原点重合，点A与点C分别放在x轴和y轴的正半轴上，则B1的坐标为：（ ）| A、（2，2，2） |
| B、（2，2，0） |
| C、（2，0，2） |
| D、（0，2，2） |
如图所示曲线是幂函数y=xa在第一象限内的图象，其中a=±| 1 |
| 2 |
A、
| ||||
B、2、
| ||||
C、-
| ||||
D、2、
|
cos480°的值为（ ）
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
设i是虚数单位，则复数z=i（-2+i）的虚部为（ ）
| A、-2 | B、-1 | C、-2i | D、2i |