题目内容
经过曲线y=x3-sinx+1上的一点（0，1）处的切线方程是 ．
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：对y=x3-sinx+1进行求导，求在x=0处的切线的斜率，根据点斜式，写出曲线在点x=0处的切线方程．
解答：
解：∵y=x3-sinx+1，
∴y′=3x2-cosx，
∴在x=0处的切线斜率k=f′（0）=0-cos0=-1，
又f（0）=1，
∴在点（0，1）处的切线方程为：y-1=-x，
∴y=-x+1，
故答案为：y=-x+1．
∴y′=3x2-cosx，
∴在x=0处的切线斜率k=f′（0）=0-cos0=-1，
又f（0）=1，
∴在点（0，1）处的切线方程为：y-1=-x，
∴y=-x+1，
故答案为：y=-x+1．
点评：此题主要考查利用导数研究曲线上某点处的切线方程，解此题的关键是要对f（x）能够正确求导，此题是一道基础题．
练习册系列答案
相关题目
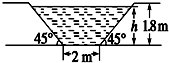如图，某灌溉渠的横断面是等腰梯形，底宽为2m，渠深为1.8m，斜坡的倾斜角是45°．（临界状态不考虑）