题目内容
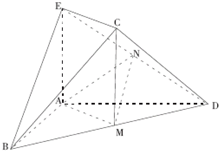 (2013•合肥二模)如图,在几何体ABCDE中,AB=AD=2,AB丄AD,AD丄平面ABE.M为线段BD的中点,MC∥AE,AE=MC=
(2013•合肥二模)如图,在几何体ABCDE中,AB=AD=2,AB丄AD,AD丄平面ABE.M为线段BD的中点,MC∥AE,AE=MC=| 2 |
(I)求证:平面BCE丄平面CDE;
(II)若N为线段DE的中点,求证:平面AMN∥平面BEC.
分析:(I)利用面面垂直的判定定理在平面BCE内找一条直线与平面CDE垂直即可证明;
(II)通过BD中点M,ED的中点N,利用三角形的中位线定理及面面平行的判定定理即可证明.
(II)通过BD中点M,ED的中点N,利用三角形的中位线定理及面面平行的判定定理即可证明.
解答: 解:(I)∵AB=AD=2,AB丄AD,M为线段BD的中点,
解:(I)∵AB=AD=2,AB丄AD,M为线段BD的中点,
∴AM=
BD
,AM⊥BD.
∵AE=MC=
,∴AE=MC=
BD=
,∴BC⊥CD,
∵AE丄平面ABD,MC∥AE,
∴MC⊥平面ABD,∴平面CBD⊥平面ABD,∴AM⊥平面CDB.
又MC∥AE,AE=MC=
,∴四边形AMCE是平行四边形,
∴EC∥AM,∴EC⊥平面CDB.∴BC⊥EC,∵EC∩CD=C
又∵BC⊥平面CDE,
∴平面BCE⊥平面CDE.
(II)∵BD中点M,ED的中点N,∴MN∥BE,
又∵MN?平面BCE,BE?平面BCE,
∴MN∥平面BEC
由(I)知EC∥AM,又∵AM?平面BCE,EC?平面BCE,
∴AM∥平面BEC,且AM∩MN=M.
∴平面AMN∥平面BEC.
 解:(I)∵AB=AD=2,AB丄AD,M为线段BD的中点,
解:(I)∵AB=AD=2,AB丄AD,M为线段BD的中点,∴AM=
| 1 |
| 2 |
| 2 |
∵AE=MC=
| 2 |
| 1 |
| 2 |
| 2 |
∵AE丄平面ABD,MC∥AE,
∴MC⊥平面ABD,∴平面CBD⊥平面ABD,∴AM⊥平面CDB.
又MC∥AE,AE=MC=
| 2 |
∴EC∥AM,∴EC⊥平面CDB.∴BC⊥EC,∵EC∩CD=C
又∵BC⊥平面CDE,
∴平面BCE⊥平面CDE.
(II)∵BD中点M,ED的中点N,∴MN∥BE,
又∵MN?平面BCE,BE?平面BCE,
∴MN∥平面BEC
由(I)知EC∥AM,又∵AM?平面BCE,EC?平面BCE,
∴AM∥平面BEC,且AM∩MN=M.
∴平面AMN∥平面BEC.
点评:本题主要考查平面图形中的线线关系,线面平行和线面垂直的判定宝理.熟练掌握线面、面面平行与垂直的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目