题目内容
 如图1所示,在边长为12的正方形ADD1A1中,点B,C在线段AD上,且AB=3,BC=4,作BB1∥AA1,分别交A1D1,AD1于点B1,P,作CC1∥AA1,分别交A1D1,AD1于点C1,Q,将该正方形沿BB1,CC1折叠,使得DD1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.
如图1所示,在边长为12的正方形ADD1A1中,点B,C在线段AD上,且AB=3,BC=4,作BB1∥AA1,分别交A1D1,AD1于点B1,P,作CC1∥AA1,分别交A1D1,AD1于点C1,Q,将该正方形沿BB1,CC1折叠,使得DD1与AA1重合,构成如图2所示的三棱柱ABC-A1B1C1.(1)求证:AB⊥平面BCC1B1;
(2)若点E为四边形BCQP内一动点,且二面角E-AP-Q的余弦值为
| ||
| 3 |
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)在正方形ADD1A1中,由已和知得三棱柱ABC-A1B1C1的底面三角形ABC的边AC=5.AB⊥BC.由此能证明⊥平面BCC1B1.
(2)以B为原点,建立如图所示的空间直角坐标系B-xyz,利用向量法能求出|BE|的最小值为点B,到线段:m+2n-6=0 的距离
.
(2)以B为原点,建立如图所示的空间直角坐标系B-xyz,利用向量法能求出|BE|的最小值为点B,到线段:m+2n-6=0 的距离
6
| ||
| 5 |
解答:
解:(1)在正方形ADD1A1中,∵CD=AD-AB-BC=5,
∴三棱柱ABC-A1B1C1的底面三角形ABC的边AC=5.
∵AB=3,BC=4,∴AB2+BC2=AC2,
∴AB⊥BC.
∵四边形ADD1A1为正方形,AA1∥BB1,
∴AB⊥BB1,而BC∩BB1=B,
∴AB⊥平面BCC1B1.(4分)
(2)∵AB,BC,BB1两两互相垂直.
以B为原点,建立如图所示的空间直角坐标系B-xyz,
则A(0,0,3),B(0,0,0),C(4,0,0),P(0,3,0),Q(4,7,0),
∴
=(0,3,-3),
=(4,7,-3),
设平面PQA的一个法向量为
=(x,y,z).
则由
,
令x=-1,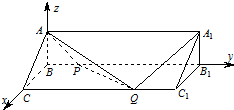 得y=z=1.所以
得y=z=1.所以
=(-1,1,1).
设点E(m,n,0),则
=(m,n,3),
=(m,n-3,0),设平面EAP的法向量
=(x,y,z),
由
,得
=(3-n,m,m),
∵二面角E-AP-Q的余弦值为
,
∴cos<
,
>=
=
,
得:m+2n-6=0
∴|BE|的最小值为点B,到线段:m+2n-6=0 的距离
.(13分)
∴三棱柱ABC-A1B1C1的底面三角形ABC的边AC=5.
∵AB=3,BC=4,∴AB2+BC2=AC2,
∴AB⊥BC.
∵四边形ADD1A1为正方形,AA1∥BB1,
∴AB⊥BB1,而BC∩BB1=B,
∴AB⊥平面BCC1B1.(4分)
(2)∵AB,BC,BB1两两互相垂直.
以B为原点,建立如图所示的空间直角坐标系B-xyz,
则A(0,0,3),B(0,0,0),C(4,0,0),P(0,3,0),Q(4,7,0),
∴
| AP |
| AQ |
设平面PQA的一个法向量为
| n |
则由
|
令x=-1,
 得y=z=1.所以
得y=z=1.所以| n |
设点E(m,n,0),则
| AE |
| PE |
| m |
由
|
| m |
∵二面角E-AP-Q的余弦值为
| ||
| 3 |
∴cos<
| m |
| n |
| n-3+2m | ||||
|
| ||
| 3 |
得:m+2n-6=0
∴|BE|的最小值为点B,到线段:m+2n-6=0 的距离
6
| ||
| 5 |
点评:本题考查直线与平面垂直的证明,考查线段的最小值的求法,考查点到线段的距离的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知
=
,则a•b=( )
| lim |
| x→1 |
| x-1 |
| x2+ax+b |
| 1 |
| 4 |
| A、-6 | B、-5 | C、5 | D、6 |