题目内容

已知椭圆C：
x2
a2
+
y2
b2
=1，经过p（1，
3
2
），离心率为
3
2
，求椭圆的方程．
考点：椭圆的标准方程
专题：圆锥曲线的定义、性质与方程
分析：由已知得
1
a2
+
3
4b2
=1
c
a
=
3
2
a2=b2+c2
，由此能求出椭圆的方程．
解答： 解：∵椭圆C：
x2
a2
+
y2
b2
=1，经过p（1，
3
2
），离心率为
3
2
，
∴
1
a2
+
3
4b2
=1
c
a
=
3
2
a2=b2+c2
，解得a=2，c=
3
，b=1，
∴椭圆的方程为
x2
4
+y2=1．
点评：本题考查椭圆方程的求法，是基础题，解题时要注意椭圆性质的合理运用．
练习册系列答案
相关题目
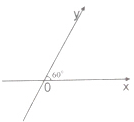如图所示，∠xoy=60°，
e1
，
e2
，分别是与x轴、y轴正方向相同的单位向量，若
m
=x
e1
+y
e2
，记
m
=（x，y），设
a
=（p，q），若
a
的模长为1，则p+q的最大值是（　　）
A、1
B、
2
3
3
C、C
2
2
D、
4
3
已知命题p：x2-2x-2≥1；命题q：0＜x＜4，若“p∨q”为真．“p∧q”为假．求实数x的取值范围．
已知函数f（x）=-x2+x，则f（x）从-1到-0.9的平均变化率为（　　）
A、3B、0.29
C、2.09D、2.9
已知角θ终边上一点P的坐标为（x，3），x≠0，且cosθ=
10
10
x，求sinθ和cosθ．
（1）若角α的终边落在直线y=x上，求值：
sinα
1-sin2α
+
1-cos2α
cosα
；
（2）求证：2（1+cosα）=
(1-sinα+cosα)2
1-sinα
．
已知sinθ+sinθ=1，求cosθ+cosθ+cosθ的值；
已知α是△ABC的内角，且sinα+cosα=
3
2
，求cosα-sinα的值．
设集合A={x|kπ-
π
4
≤x≤kπ+
π
4
，k∈Z}，B={x|x2≤36}，试求A∩B．
在三角形ABC中，角A，B，C所对的边a，b，c，若a=
3
，b=
2
，asinBcosC+csinBcosA=
2
2b
，则角A
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网