题目内容
.(本题满分13分)设函数 ,方程f(x)=x有唯一的解,
,方程f(x)=x有唯一的解,
已知f(xn)=xn+1(n∈N﹡)且f(xl)= .
.
(1)求证:数列{ )是等差数列;
)是等差数列;
(2)若 ,求Sn=b1+b2+b3+…+bn
,求Sn=b1+b2+b3+…+bn
(3)在(2)的条件下,是否存在最小正整数m,使得对任意n∈N﹡,有 成立,若存在,求出m的值;若不存在,请说明理由。
成立,若存在,求出m的值;若不存在,请说明理由。
【答案】
解:(1)证明:由题意得: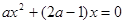
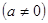 有唯一解,得
有唯一解,得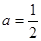
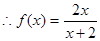 ,
,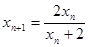
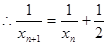 ,即
,即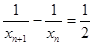
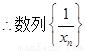 为等差数列
………………………4分
为等差数列
………………………4分
(2)又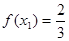 ,即
,即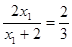 ,解得
,解得
故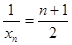 ,即
,即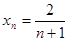
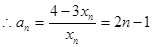 ,
,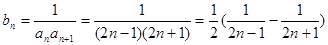
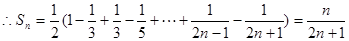 ………………………8分
………………………8分
(3)由(2)得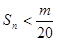 ,即为
,即为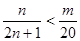
得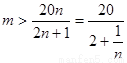 ,而
,而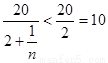 ,故
,故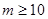
即最小的正整数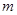 的值为10.
………………………13分
的值为10.
………………………13分
【解析】略

练习册系列答案
相关题目
 ,
, ,
, .
.  ,
, ; (2) 若
; (2) 若 ,求
,求 的取值范围.
的取值范围. 的三个内角
的三个内角 依次成等差数列.
依次成等差数列. ,试判断
,试判断 ,求
,求
 中,
中, ,
, ,
, 分别为内角
分别为内角 ,
, ,
, 所对的边,且满足
所对的边,且满足 .
. ,且
,且 ,
, ,求
,求 的值.
的值. 展开式中,求:
展开式中,求: 平面ABCD,AD//BC//FE,AB
平面ABCD,AD//BC//FE,AB AD.
AD. ?若存在,试确定点M的位置;若不存在,请说明理由.
?若存在,试确定点M的位置;若不存在,请说明理由.