题目内容
设e1、e2分别为具有公共焦点F1、F2的椭圆和双曲线的离心率，P是两曲线的一个公共点，且满足|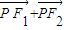
|=|
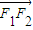|，则
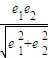的值为（ ）A．
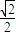
B．2
C．
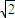
D．1
【答案】分析：利用|
|=|
|，可知∠F1PF2=90°，设|PF1|=m，|PF2|=n，|F1F2|=2c，不妨设m＞n，可得m2+n2=4c2，求出
，
，再求出平方倒数的和，即可得到结论．
解答：解：设|PF1|=m，|PF2|=n，|F1F2|=2c，
不妨设m＞n，由|
|=|
|，可知∠F1PF2=90°
∴m2+n2=4c2，
∵
，
∴
∴
=
故选A．
点评：本题考查圆锥曲线的共同特征，考查圆锥曲线的离心率，正确求出离心率是关键．
|=||，可知∠F1PF2=90°，设|PF1|=m，|PF2|=n，|F1F2|=2c，不妨设m＞n，可得m2+n2=4c2，求出，，再求出平方倒数的和，即可得到结论．解答：解：设|PF1|=m，|PF2|=n，|F1F2|=2c，
不妨设m＞n，由|
|=||，可知∠F1PF2=90°∴m2+n2=4c2，
∵
，∴
∴
=故选A．
点评：本题考查圆锥曲线的共同特征，考查圆锥曲线的离心率，正确求出离心率是关键．
练习册系列答案
活力试卷系列答案
课课优能力培优100分系列答案
相关题目