题目内容
6.若正三棱锥P-ABC(底面是正三角形,顶点P在底面的射影是△ABC的中心)满足|$\overrightarrow{PA}$+$\overrightarrow{PB}$|=|$\overrightarrow{AB}$|=4$\sqrt{3}$,则该三棱锥外接球球心O到平面ABC的距离为$\sqrt{2}$.分析 由题意,PA,PB,PC两两垂直,PA=PB=PC=2$\sqrt{6}$,AB=4$\sqrt{3}$,如图所示,将P-ABC视为正方体的一部分,球的半径R=3$\sqrt{2}$,OP=2$\sqrt{2}$,即可求出该三棱锥外接球球心O到平面ABC的距离.
解答 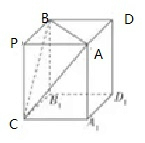 解:由题意,PA,PB,PC两两垂直,PA=PB=PC=2$\sqrt{6}$,AB=4$\sqrt{3}$,
解:由题意,PA,PB,PC两两垂直,PA=PB=PC=2$\sqrt{6}$,AB=4$\sqrt{3}$,
如图所示,将P-ABC视为正方体的一部分,球的半径R=3$\sqrt{2}$,
OP=2$\sqrt{2}$,
所以该三棱锥外接球球心O到平面ABC的距离为3$\sqrt{2}$-2$\sqrt{2}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题主要考查球内接多面体的性质的应用,考查了计算能力和数形结合思想,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
4.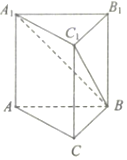 《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )
《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )
 《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )
《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )| A. | $\frac{8}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
2.若命题“p∧(¬q)”与“¬p”均为假命题,则( )
| A. | p真q真 | B. | p假q真 | C. | p假q假 | D. | p真q假 |
15.设随机变量ξ等可能取值1,2,3,4,…,n,如果p(ξ<4)=0.3,则n的值为( )
| A. | 3 | B. | 4 | C. | 10 | D. | 不能确定 |
16.在等差数列{an}中,a1=-2 012,其前n项和为Sn,若$\frac{{{S_{12}}}}{12}-\frac{{{S_{10}}}}{10}$=2,则S2012的值等于( )
| A. | -2 011 | B. | -2 012 | C. | -2 010 | D. | -2 013 |