题目内容
设等比数列{an}满足公比q∈N*,an∈N*,且{an}中的任意两项之积也是该数列中的一项,若a1=281,则q的所有可能取值的集合为 .
【答案】分析:依题意可求得该等比数列的通项公式an,设该数列中的任意两项为am,at,它们的积为ap,求得q=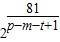 ,分析即可.
,分析即可.
解答:解:由题意,an=281qn-1,设该数列中的任意两项为am,at,它们的积为ap,
则为am•at=ap,即281qm-1•281qt-1=281•qp-1,(q,m,t,p∈N*),
∴q=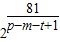 ,
,
故p-m-t+1必是81的正约数,
即p-m-t+1的可能取值为1,3,9,27,81,
即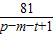 的可能取值为1,3,9,27,81,
的可能取值为1,3,9,27,81,
所以q的所有可能取值的集合为{281,227,29,23,2}
点评:本题考查等比数列的通项公式,依题意求得q=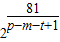 是难点,分析得到p-m-t+1必是81的正约数是关键,考查分析与运算能力,属于难题.
是难点,分析得到p-m-t+1必是81的正约数是关键,考查分析与运算能力,属于难题.
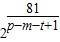 ,分析即可.
,分析即可.解答:解:由题意,an=281qn-1,设该数列中的任意两项为am,at,它们的积为ap,
则为am•at=ap,即281qm-1•281qt-1=281•qp-1,(q,m,t,p∈N*),
∴q=
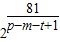 ,
,故p-m-t+1必是81的正约数,
即p-m-t+1的可能取值为1,3,9,27,81,
即
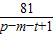 的可能取值为1,3,9,27,81,
的可能取值为1,3,9,27,81,所以q的所有可能取值的集合为{281,227,29,23,2}
点评:本题考查等比数列的通项公式,依题意求得q=
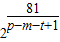 是难点,分析得到p-m-t+1必是81的正约数是关键,考查分析与运算能力,属于难题.
是难点,分析得到p-m-t+1必是81的正约数是关键,考查分析与运算能力,属于难题. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
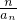 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.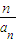 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.