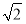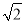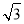Question

已知椭圆C1：＋y2＝1，椭圆C2以C1的长轴为短轴，且与C1有相同的离心率．

(1)求椭圆C2的方程；

(2)设O为坐标原点，点A，B分别在椭圆C1和C2上，＝2，求直线AB的方程．

 

Answer 1

（1）＝1（2）y＝x或y＝－x

【解析】(1)由已知可设椭圆C2的方程为＝1(a>2)，

其离心率为，故＝，解得a＝4.故椭圆C2的方程为＝1.

(2)A，B两点的坐标分别记为(xA，yA)，(xB，yB)，

由＝2及(1)知，O，A，B三点共线且点A，B不在y轴上，因此可设直线AB的方程为y＝kx.

将y＝kx代入＋y2＝1中，得(1＋4k2)x2＝4，所以.

将y＝kx代入＝1中，得(4＋k2)x2＝16，所以.

又由＝2，得，

∴，解得k＝±1.

故直线AB的方程为y＝x或y＝－x.