题目内容
在△ABC中,a=3 ,b=2
,b=2 ,cos C=
,cos C= ,则△ABC的面积为( ).
,则△ABC的面积为( ).
A.3 | B.2 | C.4 | D. |
C
解析试题分析:因为,a=3 ,b=2
,b=2 ,cos C=
,cos C= ,所以,△ABC的面积为
,所以,△ABC的面积为 4
4 ,故选C。
,故选C。
考点:本题主要考查三角形面积公式,三角函数同角公式。
点评:简单题,△ABC的面积为两边长及其夹角正弦乘积的一半。

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
 中,角
中,角 、
、 、
、 所以的边为
所以的边为 、
、 、
、 , 若
, 若 ,
, ,
, 面积
面积 ,则
,则 ( )
( )
A. | B. | C. | D. |
在△ABC中,三个内角A,B,C的对边分别为 ,若
,若 ,则内角A的值为( )
,则内角A的值为( )
A. 或 或 | B. 或 或 | C. | D. |
在△ABC中,若 ,则△
,则△ 是( )
是( )
| A.等边三角形 | B.等腰三角形 | C.不等边三角形 | D.直角三角形 |
在△ABC中,根据下列条件解三角形,则其中有两个解的是
A.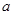 = 14,b = 16,A = 45° = 14,b = 16,A = 45° | B.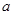 = 60,c = 48,B = 100° = 60,c = 48,B = 100° |
C.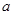 = 7,b = 5,A = 80° = 7,b = 5,A = 80° | D.b = 10,A = 45°,B = 70° |
 ABC中,a=6,B=30
ABC中,a=6,B=30 ,C=120
,C=120 ,则
,则 ABC的面积为
ABC的面积为
| A.9 | B.8 | C.9 | D.18 |
若一个三角形的三内角的度数既成等差数列,又成等比数列,则这个三角形的形状为 ( )
| A.直角三角形 | B.钝角三角形 | C.等腰三角形 | D.等边三角形 |
 ,则角A等于( )
,则角A等于( )



 中角A、B、C的对边分别是a、b、c,
中角A、B、C的对边分别是a、b、c, ,则三角形是( )
,则三角形是( )