题目内容
ABC中，a=6,B=30
,C=120,则ABC的面积为
| A．9 | B．8 | C．9 | D．18 |
C
解析试题分析：利用三角形的内角和公式求得A=30°，可得△ABC为等腰三角形，直接利用△ABC的面积，求得结果．解：∵△ABC中，a=6，B=30°，C=120°，∴A=30°．故△ABC为等腰三角形，故b=6，则△ABC的面积为
×6×6×sin120°=9，故选C
考点：正弦定理
点评：本题考查三角形中的几何计算，也可以利用正弦定理求解，是一道基础题．
练习册系列答案
综合自测系列答案
相关题目
某人要制作一个三角形，要求它的三条高的长度分别是
，则此人 （ ）
| A．不能作出这样的三角形 | B．能作出一个锐角三角形 |
| C．能作出一个直角三角形 | D．能作出一个钝角三角形 |
在△ABC中，a＝3
，b＝2
，cos C＝
，则△ABC的面积为( )．
| A．3 | B．2 | C．4 | D． |
在不等边三角形中，a是最大的边，若
，则角A的取值范围为（ ）
A． | B． | C． | D． |
在△ABC中，
则最短边的边长为（ ）
A． | B． | C． | D． |
已知△ABC满足
， 则角C的大小为（ ）
A． | B． | C． | D． |
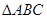中，若
，
，
，则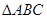的面积为（ ）
A． | B． | C．或 | D．或 |
如图，一条河的两岸平行，河的宽度
m，一艘客船从码头
出发匀速驶往河对岸的码头
.
已知
km，水流速度为
km/h, 若客船行驶完航程所用最短时间为
分钟，则客船在静水中的速度大小为
A． km/h | B． km/h |
C． km/h | D． km/h |
在
的对边分别为
，若
成等差数列则
（ ）
A． | B． | C． | D． |