题目内容
中角A、B、C的对边分别是a、b、c，
，则三角形是（ ）
A. 直角三角形 B. 等腰或直角三角形
C. 等腰三角形 D. 等边三角形
B
解析试题分析：根据题意，由于，那么根据正弦定理可知
故可知三角形A=B,A+B=
,故该三角形是等腰或直角三角形，因此选B.
考点：正弦定理
点评：本题主要看考查了正弦定理及两角和与差的三角公式在三角形的形状的判断中的综合应用，属于公式的简单综合
练习册系列答案
相关题目
符合下列条件的三角形有且只有一个的是
A． | B． |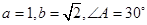
C． | D． |
设
是
的面积，
的对边分别为
，且
，
则 （ ）
| A．是钝角三角形 |
| B．是锐角三角形 |
| C．可能为钝角三角形，也可能为锐角三角形 |
| D．无法判断 |
在△ABC中，a＝3
，b＝2
，cos C＝
，则△ABC的面积为( )．
| A．3 | B．2 | C．4 | D． |
在△
中，
，
，
，则
A． | B． | C． | D． |
在不等边三角形中，a是最大的边，若
，则角A的取值范围为（ ）
A． | B． | C． | D． |
在△ABC中，
则最短边的边长为（ ）
A． | B． | C． | D． |
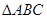中，若
，
，
，则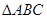的面积为（ ）
A． | B． | C．或 | D．或 |
等腰三角形一腰上的高是
，这条高与底边的夹角为
，则底边长=（ ）
| A．2 | B． | C．3 | D． |