题目内容
【题目】如图,已知抛物线![]() 的焦点为
的焦点为![]() ,椭圆
,椭圆![]() 的中心在原点,
的中心在原点,![]() 为其右焦点,点
为其右焦点,点![]() 为曲线
为曲线![]() 和
和![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为抛物线
为抛物线![]() 上的两个动点,且使得线段
上的两个动点,且使得线段![]() 的中点
的中点![]() 在直线
在直线![]() 上,
上,
![]() 为定点,求
为定点,求![]() 面积的最大值.
面积的最大值.
【答案】(1)椭圆![]() 的标准方程为
的标准方程为![]() ; (2)
; (2)![]() 面积的最大值为
面积的最大值为![]() .
.
【解析】
试题分析:(1)由已知得![]() ,跟据抛物线定义,得
,跟据抛物线定义,得![]() ,所以点
,所以点![]() ;据椭圆定义,得
;据椭圆定义,得![]() .
.
所以椭圆![]() 的标准方式是
的标准方式是![]() .(2)因为
.(2)因为![]() 为线段
为线段![]() 的中点,得直线
的中点,得直线![]() 的方程为
的方程为![]() ;联立
;联立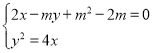 ,得
,得![]() ,由弦长公式
,由弦长公式![]() 和点
和点![]() 到直线
到直线![]() 的距离,得
的距离,得![]() .
.
再根据函数的单调性得![]() 面积的最大值为
面积的最大值为![]() .
.
试题解析:(1)设椭圆![]() 的方程为
的方程为![]() ,半焦距为
,半焦距为![]() .
.
由已知,点![]() ,则
,则![]() .
.
设点![]()
![]() ,据抛物线定义,得
,据抛物线定义,得![]() .由已知,
.由已知,![]() ,则
,则![]() .
.
从而![]() ,所以点
,所以点![]() .
.
设点![]() 为椭圆的左焦点,则
为椭圆的左焦点,则![]() ,
,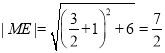 .
.
据椭圆定义,得![]() ,则
,则![]() .
.
从而![]() ,所以椭圆
,所以椭圆![]() 的标准方式是
的标准方式是![]() .
.
(2)设点![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
两式相减,得![]() ,即
,即![]() .因为
.因为![]() 为线段
为线段![]() 的中点,则
的中点,则![]() .
.
所以直线![]() 的斜率
的斜率![]() .
.
从而直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
联立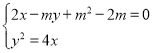 ,得
,得![]() ,则
,则![]() .
.
所以![]() .
.
设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则![]() .
.
所以![]() .
.
由![]() ,得
,得![]() .令
.令![]() ,则
,则![]()
![]() .
.
设![]()
![]() ,则
,则![]() .
.
由![]() ,得
,得![]() .从而
.从而![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数,
上是减函数,
所以![]() ,故
,故![]() 面积的最大值为
面积的最大值为![]() .
.

练习册系列答案
相关题目