题目内容
3.已知直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=BB1,求异面直线A1B与B1C所成的角60°.分析 以B为原点,BA为x轴,BC为y轴,BB1为z轴,建立空间直角坐标系,利用向量法能求出异面直线A1B与B1C所成的角.
解答 解:以B为原点,BA为x轴,BC为y轴,BB1为z轴,建立空间直角坐标系,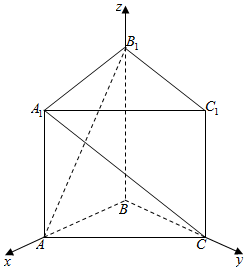
设AB=BC=BB1=1,
则A1(1,0,1),B(0,0,0),B1(0,0,1),C(0,1,0),
$\overrightarrow{{A}_{1}B}$=(-1,0,-1),$\overrightarrow{{B}_{1}C}$=(0,1,-1),
设异面直线A1B与B1C所成的角为θ,
cosθ=$\frac{|\overrightarrow{{A}_{1}B}•\overrightarrow{{B}_{1}C}|}{|\overrightarrow{{A}_{1}B}|•|\overrightarrow{{B}_{1}C}|}$=$\frac{1}{\sqrt{2}×\sqrt{2}}$=$\frac{1}{2}$,
∴θ=60°.
∴异面直线A1B与B1C所成的角为60°.
故答案为:60°.
点评 本题考查异面直线所成成角的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
13.若复数z满足z=$\frac{|8+6i|}{6-8i}$(i是虚数单位),则z的虚部为( )
| A. | 4 | B. | $\frac{4}{5}$ | C. | -4 | D. | -$\frac{4}{5}$ |
14.若实数x,y满足不等式组$\left\{\begin{array}{l}x+3y-3≤0\\ x-y+1≥0\\ y≥1\end{array}\right.$,则z=2|x|+y的取值范围是( )
| A. | [-1,3] | B. | [1,3] | C. | [-1,11] | D. | [-5,11] |
18.已知复数w满足w-1=(1+w)i(i为虚数单位),则w=( )
| A. | 1-i | B. | -i | C. | -1+i | D. | i |
15.“a>1”是当“0<x≤2时,2-2x≥logax成立”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
12.若函数f(x)=sin(x+φ)是偶函数,则φ的一个值是( )
| A. | 0 | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
13.下列函数在其定义域内既是奇函数又是增函数的是( )
| A. | y=2x | B. | y=x3+x | C. | $y=-\frac{1}{x}$ | D. | y=-log2x |