题目内容
将函数f(x)=sin(2x+θ)(-
<θ<
)的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x)、g(x)的图象都经过点P(0,
),则φ的值可以是 .
| π |
| 2 |
| π |
| 2 |
| ||
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由f(x)的图象经过点P(0,
),且-
<θ<
,可得θ=
,又由g(x)的图象也经过点P(0,
),可求出满足条件的φ的值.
| ||
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
| ||
| 2 |
解答:
函数f(x)=sin(2x+θ)(-
<θ<
)向右平移φ个单位,得到g(x)=sin(2x+θ-2φ),
因为两个函数都经过P(0,
),
所以sinθ=
,
又因为-
<θ<
,
所以θ=
,
所以g(x)=sin(2x+
-2φ),
sin(
-2φ)=
,
所以
-2φ=2kπ+
,k∈Z,此时φ=kπ,k∈Z,
或
-2φ=2kπ+
,k∈Z,此时φ=kπ-
,k∈Z,
故答案为:
,(答案不唯一)
| π |
| 2 |
| π |
| 2 |
因为两个函数都经过P(0,
| ||
| 2 |
所以sinθ=
| ||
| 2 |
又因为-
| π |
| 2 |
| π |
| 2 |
所以θ=
| π |
| 3 |
所以g(x)=sin(2x+
| π |
| 3 |
sin(
| π |
| 3 |
| ||
| 2 |
所以
| π |
| 3 |
| π |
| 3 |
或
| π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
故答案为:
| 5π |
| 6 |
点评:本题考查的知识点是函数y=Asin(ωx+φ)的图象变换,三角函数求值,难度中档.

练习册系列答案
相关题目
如果a=30.2,b=log0.23,c=0.23,那么它们之间的大小关系是( )
| A、b<a<c |
| B、a<b<c |
| C、b<c<a |
| D、c<b<a |
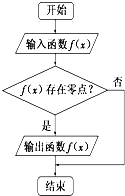 执行如图所示的程序框图,若输入如下四个函数:
执行如图所示的程序框图,若输入如下四个函数: