题目内容
20.已知指数函数f(x)=ax-16+7(a>0且a≠1)的图象恒过定点P,若定点P在幂函数g(x)的图象上,则幂函数g(x)的图象是( )| A. |  | B. | 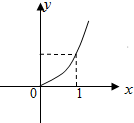 | ||
| C. | 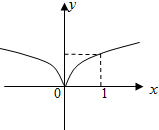 | D. |  |
分析 求出定点P,然后求解幂函数的解析式,即可得出结论.
解答 解:指数函数f(x)=ax-16+7(a>0且a≠1)的图象恒过定点P,
令x-16=0,解得x=16,
且f(16)=1+7=8,
所以f(x)的图象恒过定点P(16,8);
设幂函数g(x)=xa,P在幂函数g(x)的图象上,
可得:16a=8,解得a=$\frac{3}{4}$;
所以g(x)=${x}^{\frac{3}{4}}$,
幂函数g(x)的图象是A.
故选:A.
点评 本题考查了指数函数与幂函数的性质与应用问题,也考查了计算能力的问题,是基础题.

练习册系列答案
相关题目
11.正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,在正方体表面上与点A距离是2的点形成一条封闭的曲线,这条曲线的长度是( )
| A. | π | B. | $\frac{3}{2}π$ | C. | 3π | D. | $\frac{5}{2}π$ |
15.在高台跳水运动中,已知运动员相对于水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t)=-4.9t2+6.5t+10,则运动员在t=1s时的瞬间速度为( )
| A. | -3.3 m/s | B. | 3.3 m/s | C. | -11.6 m/s | D. | 11.6 m/s |
12.设x∈(0,π),若$\frac{1}{sinx}+\frac{1}{cosx}=2\sqrt{2}$,则$sin(2x+\frac{π}{3})$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |