题目内容
已知数列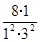 ,
,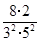 ,…,
,…,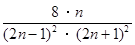 ,….S
,….S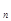 为其前n项和,求S
为其前n项和,求S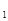 、S
、S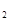 、S
、S 、S
、S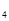 ,推测S
,推测S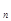 公式,并用数学归纳法证明.
公式,并用数学归纳法证明.
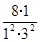 ,
,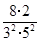 ,…,
,…,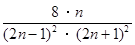 ,….S
,….S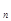 为其前n项和,求S
为其前n项和,求S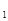 、S
、S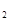 、S
、S 、S
、S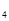 ,推测S
,推测S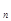 公式,并用数学归纳法证明.
公式,并用数学归纳法证明.S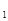 =
= ,S
,S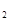 =
= ,S
,S =
= ,S
,S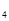 =
= 。证明见解析
。证明见解析
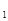 =
= ,S
,S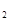 =
= ,S
,S =
= ,S
,S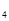 =
= 。证明见解析
。证明见解析根据已知条件先求解前几项,然后归纳猜想得到结论,并运用数学归纳法分为两步骤来进行,注意要用到假设以及n=k,n=k+1之间的变化的综合运用。
解:S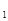 =
= ,S
,S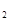 =
= ,S
,S =
= ,S
,S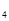 =
= ,猜测S
,猜测S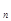 =
= (n∈N
(n∈N )
)
①当n=1时,等式显然成立;
②假设当n=k时等式成立,即:S =
= ,
,
当n=k+1时,S =S
=S +
+ =
= +
+
= =
= =
= ,
,
即n=k+1时等式也成立.综上①②,等式对任何n∈N 都成立.
都成立.
解:S
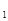 =
= ,S
,S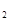 =
= ,S
,S =
= ,S
,S =
= ,猜测S
,猜测S =
= (n∈N
(n∈N )
)①当n=1时,等式显然成立;
②假设当n=k时等式成立,即:S
 =
= ,
,当n=k+1时,S
 =S
=S +
+ =
= +
+
=
 =
= =
= ,
,即n=k+1时等式也成立.综上①②,等式对任何n∈N
 都成立.
都成立.
练习册系列答案
相关题目
 (
(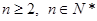 ),
),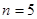 时,求
时,求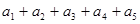 的值;
的值; ,试用数学归纳法证明:
,试用数学归纳法证明: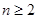 时,
时, 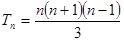 。
。 当
当 时,试猜想
时,试猜想 的值,并用数学归纳法给予证明。
的值,并用数学归纳法给予证明。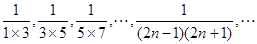 ,计算
,计算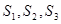 ,根据计算结果,猜想
,根据计算结果,猜想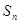 的表达式,并用数学归纳法给出证明.
的表达式,并用数学归纳法给出证明.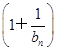 (其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与
(其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论. 对任意实数x 、y都有
对任意实数x 、y都有 ,
, 的值;
的值; ,求
,求 、
、 、
、 的值;
的值;
 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。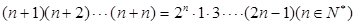 ,从“k到k+1”左端需增乘的代数式为( )
,从“k到k+1”左端需增乘的代数式为( )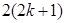
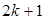
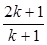
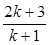
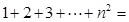
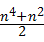 ,则当n=k+1时左端应在n=k的基础上增加 ( )
,则当n=k+1时左端应在n=k的基础上增加 ( ) 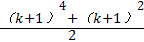
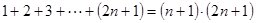 ”,在验证
”,在验证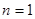 时,左边计算的值=___.
时,左边计算的值=___.